Skuteczność wspólnego rozwiązywania problemów w promowaniu krytycznego myślenia uczniów: metaanaliza oparta na literaturze empirycznej / Enwei Xu, Wei Wang & Qingxia Wang 

Chociaż krytyczne myślenie ma długą historię w badaniach, koncepcja krytycznego myślenia, która jest uważana za podstawową kompetencję uczniów w XXI wieku, ostatnio przyciągnęła więcej uwagi badaczy i praktyków nauczania (National Research Council, 2012 ). Myślenie krytyczne powinno być rdzeniem reformy programowej opartej na kluczowych kompetencjach w obszarze edukacji (Peng i Deng, 2017 ), ponieważ uczniowie z myśleniem krytycznym mogą nie tylko rozumieć znaczenie wiedzy, ale także skutecznie rozwiązywać praktyczne problemy w prawdziwym życiu nawet po zdobyciu wiedzy jest zapomniany (Kek i Huijser, 2011 ). Definicja krytycznego myślenia nie jest uniwersalna (Ennis, 1989 ; Castle, 2009; Niu i in., 2013 ). Ogólnie rzecz biorąc, definicja krytycznego myślenia to samoświadomy i samoregulujący się proces myślowy (Facione, 1990 ; Niu i in., 2013 ). Odnosi się do umiejętności poznawczych potrzebnych do interpretowania, analizowania, syntezy, rozumowania i oceny informacji, jak również tendencji do stosowania tych zdolności w stosunku do postaw (Halpern, 2001 ). Pogląd, że krytycznego myślenia można uczyć i uczyć się go poprzez nauczanie programowe, spotkał się z szerokim poparciem wielu badaczy (np. Kuncel, 2011 ; Leng i Lu, 2020 ), co doprowadziło do wysiłków nauczycieli mających na celu promowanie go wśród uczniów. W zakresie praktyki pedagogicznej wyróżnia się trzy rodzaje kursów nauczania krytycznego myślenia (Ennis,1989 ). Pierwszy to niezależny program nauczania, w ramach którego nauczane i kultywowane jest krytyczne myślenie bez angażowania wiedzy z określonych dyscyplin; drugi to zintegrowany program nauczania, w którym krytyczne myślenie jest zintegrowane z nauczaniem innych dyscyplin jako jasny cel nauczania; a trzeci to mieszany program nauczania, w którym krytyczne myślenie jest nauczane równolegle z nauczaniem innych dyscyplin w mieszanym szkoleniu nauczycielskim. Ponadto badacze i pedagodzy opracowali liczne narzędzia pomiarowe do pomiaru krytycznego myślenia w kontekście praktyki nauczania. Należą do nich znormalizowane narzędzia pomiarowe, takie jak WGCTA, CCTST, CCTT i CCTDI, które zostały zweryfikowane w powtarzanych eksperymentach i są uważane za skuteczne i wiarygodne przez międzynarodowych naukowców (Facione i Facione,1992 ). Krótko mówiąc, opisy krytycznego myślenia, w tym jego dwóch wymiarów tendencji do postaw i umiejętności poznawczych, różne rodzaje kursów nauczania i ujednolicone narzędzia pomiarowe zapewniają złożone ramy normatywne dla zrozumienia, nauczania i oceny krytycznego myślenia.

Kultywowanie krytycznego myślenia w nauczaniu programowym może rozpocząć się od problemu, a jednym z najpopularniejszych podejść do nauczania krytycznego myślenia jest uczenie się oparte na problemach (Liu i in., 2020 ). Duch i in. ( 2001 ) zauważyli, że uczenie się oparte na rozwiązywaniu problemów we współpracy grupowej jest progresywnym aktywnym uczeniem się, które może poprawić umiejętności krytycznego myślenia i rozwiązywania problemów uczniów. Wspólne rozwiązywanie problemów to organiczna integracja uczenia się opartego na współpracy i uczenia się opartego na problemach, która stawia uczniów w centrum procesu uczenia się i wykorzystuje problemy o słabej strukturze w rzeczywistych sytuacjach jako punkt wyjścia dla procesu uczenia się (Liang i in. ., 2017). Studenci zdobywają wiedzę potrzebną do rozwiązywania problemów w grupie współpracującej, osiągania konsensusu w sprawie problemów w terenie i formułowania rozwiązań za pomocą metod współpracy społecznej, takich jak dialog, interpretacja, kwestionowanie, debata, negocjacje i refleksja, promując w ten sposób rozwój wiedza domenowa uczniów i krytyczne myślenie (Cindy, 2004 ; Liang i in., 2017 ).

Wspólne rozwiązywanie problemów było szeroko stosowane w praktyce nauczania krytycznego myślenia, a w kilku badaniach podjęto próbę przeprowadzenia systematycznego przeglądu i metaanalizy literatury empirycznej na temat krytycznego myślenia z różnych perspektyw. Jednak niewiele uwagi poświęcono wpływowi wspólnego rozwiązywania problemów na krytyczne myślenie. Dlatego najlepszym podejściem do rozwijania i wzmacniania krytycznego myślenia podczas wspólnego rozwiązywania problemów jest zbadanie, jak wdrożyć instrukcje krytycznego myślenia; jednak kwestia ta jest nadal niezbadana, co oznacza, że ​​wielu nauczycieli nie jest w stanie lepiej uczyć krytycznego myślenia (Leng i Lu, 2020 ; Niu i in., 2013 ). Na przykład Huber ( 2016) przedstawili wyniki metaanalizy 71 publikacji na temat zdobywania krytycznego myślenia w różnych ramach czasowych na studiach w celu ustalenia, czy krytycznego myślenia naprawdę można się nauczyć. Autorzy ci stwierdzili, że uczniowie znacznie poprawiają swoje krytyczne myślenie na studiach i że krytyczne myślenie różni się w zależności od czynników, takich jak strategie nauczania, czas trwania interwencji, dziedzina i rodzaj nauczania. Przydatność wspólnego rozwiązywania problemów we wspieraniu krytycznego myślenia uczniów nie została jednak określona w tym badaniu ani nie ujawniła, czy istniały znaczące różnice między różnymi elementami. Metaanalizę 31 pozycji literatury edukacyjnej przeprowadzili Liu i in. ( 2020), aby ocenić wpływ rozwiązywania problemów na krytyczne myślenie studentów. Autorzy ci stwierdzili, że rozwiązywanie problemów może promować rozwój krytycznego myślenia wśród studentów i zaproponowali ustanowienie rozsądnej struktury grupowej do rozwiązywania problemów w badaniu uzupełniającym, aby poprawić krytyczne myślenie uczniów. Ponadto wcześniejsze badania empiryczne doprowadziły do ​​niejednoznacznych, a nawet sprzecznych wniosków na temat tego, czy iw jakim stopniu wspólne rozwiązywanie problemów zwiększa lub zmniejsza poziom krytycznego myślenia. Jako ilustrację, Yang i in. ( 2008) przeprowadzili eksperyment dotyczący zintegrowanego nauczania studentów college’u w oparciu o internetową tablicę ogłoszeń w celu wspierania krytycznego myślenia uczestników w kontekście wspólnego rozwiązywania problemów. Badania tych autorów ujawniły, że poprzez dzielenie się, debatowanie, badanie i refleksję nad różnymi doświadczeniami i pomysłami wspólne rozwiązywanie problemów może znacznie poprawić krytyczne myślenie uczniów w rzeczywistych sytuacjach problemowych. W przeciwieństwie do tego, wspólne rozwiązywanie problemów miało pozytywny wpływ na interakcje uczniów i mogło zwiększyć zainteresowanie nauką i motywację, ale nie mogło znacząco poprawić krytycznego myślenia uczniów w porównaniu z tradycyjnym nauczaniem w klasie, zgodnie z badaniami Nabera i Wyatta ( 2014 ) oraz Sendag i Odabasi ( 2009) odpowiednio dla uczniów szkół podstawowych i średnich.

Powyższe badania pokazują, że istnieje niespójność co do skuteczności wspólnego rozwiązywania problemów w promowaniu krytycznego myślenia uczniów. Dlatego konieczne jest przeprowadzenie dokładnego i wiarygodnego przeglądu, aby wykryć i zdecydować, czy iw jakim stopniu wspólne rozwiązywanie problemów może skutkować wzrostem lub spadkiem krytycznego myślenia. Metaanaliza to podejście do analizy ilościowej, które jest wykorzystywane do badania danych ilościowych z różnych oddzielnych badań, które koncentrują się na tym samym temacie badawczym. Podejście to charakteryzuje skuteczność jego wpływu poprzez uśrednienie wielkości efektu z wielu badań jakościowych w celu zmniejszenia niepewności wynikającej z niezależnych badań i uzyskania bardziej rozstrzygających wniosków (Lipsey i Wilson, 2001 ).

W niniejszym artykule wykorzystano podejście metaanalityczne i przeprowadzono metaanalizę w celu zbadania skuteczności wspólnego rozwiązywania problemów w promowaniu krytycznego myślenia uczniów, aby wnieść wkład zarówno w badania, jak i praktykę. Ta metaanaliza dotyczyła następujących pytań badawczych:

1. 1.Jaka jest ogólna wielkość efektu wspólnego rozwiązywania problemów w promowaniu krytycznego myślenia uczniów i jego wpływu na dwa wymiary krytycznego myślenia (tj. skłonność do postaw i umiejętności poznawcze)?
2. 2.W jaki sposób różne zmienne moderujące wpływają na rozbieżności między wnioskami z badań, jeśli wpływy różnych projektów eksperymentalnych w włączonych badaniach są heterogeniczne?

Badania te przebiegały zgodnie ze ścisłymi procedurami (np. przeszukiwanie bazy danych, identyfikacja, selekcja, kwalifikowalność, łączenie, usuwanie duplikatów i analiza włączonych badań) proponowanego przez Coopera ( 2010 ) podejścia metaanalizy do badania danych ilościowych z różnych odrębnych badań, z których wszystkie są skoncentrowane na tym samym temacie badawczym. Odpowiednie badania empiryczne, które ukazały się w światowych czasopismach edukacyjnych w XXI wieku, zostały poddane tej metaanalizie przy użyciu programu Rev-Man 5.4. Spójność danych wyodrębnionych oddzielnie przez dwóch badaczy została przetestowana przy użyciu współczynnika kappa Cohena, a na przykładowych danych przeprowadzono test obciążenia publikacji i test heterogeniczności, aby potwierdzić jakość tej metaanalizy.

Źródła danych i strategie wyszukiwania

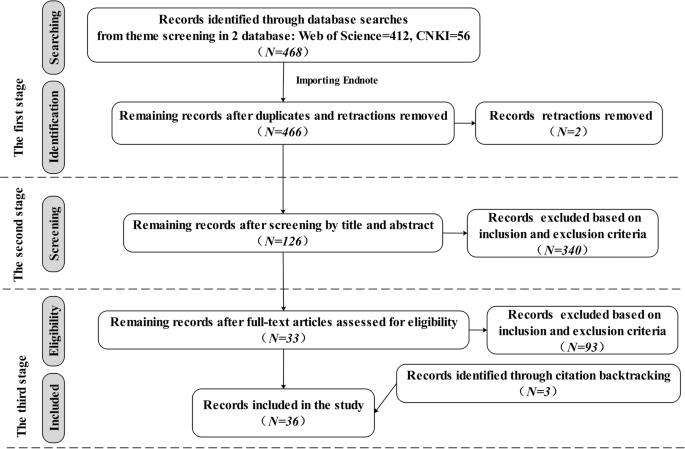
Proces zbierania danych do tej metaanalizy składał się z trzech etapów, jak pokazano na ryc. 1 , która pokazuje liczbę artykułów włączonych i wyeliminowanych podczas procesu selekcji na podstawie oświadczenia i kryteriów kwalifikowalności do badania.

Ten schemat pokazuje liczbę rekordów zidentyfikowanych, uwzględnionych i wykluczonych w artykule.

Obraz w pełnym rozmiarze

Po pierwsze, bazami danych używanymi do systematycznego wyszukiwania odpowiednich artykułów były artykuły z czasopism Web of Science Core Collection i chińskie czasopismo źródłowe Core, a także artykuły z czasopism źródłowych Chinese Social Science Citation Index (CSSCI) zawarte w CNKI. Te bazy danych zostały wybrane, ponieważ są wiarygodnymi platformami, które są źródłami naukowych i recenzowanych informacji z zaawansowanymi narzędziami wyszukiwania i zawierają literaturę związaną z tematem naszego tematu, pochodzącą od wiarygodnych badaczy i ekspertów. Wyszukiwany ciąg z operatorem boolowskim używanym w Web of Science to „TS = (((„myślenie krytyczne” lub „ct” i „pretest” lub „posttest”) lub („myślenie krytyczne” lub „ct” i „kontrola grupa” lub „quasi-eksperyment” lub „eksperyment”)) oraz („współpraca” lub „uczenie się oparte na współpracy” lub „CSCL”) oraz („rozwiązywanie problemów” lub „uczenie się oparte na problemach” lub „PBL”))). Obszar badawczy to „Edukacja Badania Edukacyjne”, a okres wyszukiwania to „od 1 stycznia 2000 r. do 30 grudnia 2021 r.”. Łącznie otrzymano 412 prac. Ciąg wyszukiwania z operatorem boolowskim używanym w CNKI to „SU = (’myślenie krytyczne’*’współpraca’ + 'myślenie krytyczne’*’uczenie się oparte na współpracy’ + 'myślenie krytyczne’*’CSCL’ + 'myślenie krytyczne’*’ rozwiązywanie problemów” + „myślenie krytyczne”* „uczenie się oparte na problemach” + „myślenie krytyczne”*„PBL” + „myślenie krytyczne”*„zorientowanie na problem”) AND FT = („eksperyment” + „quasi-eksperyment” + „test wstępny” ’ + 'posttest’ + 'badanie empiryczne’)” (przetłumaczone na chiński podczas wyszukiwania). W całym okresie wyszukiwania „styczeń 2000 do grudzień 2021” znaleziono łącznie 56 badań. Z baz danych usunięto wszelkie duplikaty i wycofania przed wyeksportowaniem bibliografii do Endnote, programu do zarządzania bibliografią. W sumie znaleziono 466 badań.

Po drugie, badania spełniające kryteria włączenia i wyłączenia z metaanalizy zostały wybrane przez dwóch badaczy po przejrzeniu abstraktów i tytułów zebranych artykułów, co dało w sumie 126 badań.

Po trzecie, dwóch badaczy dokładnie przejrzało cały tekst każdego zawartego artykułu zgodnie z kryteriami włączenia i wyłączenia. W międzyczasie przeprowadzono wyszukiwanie metodą kuli śnieżnej, korzystając z odniesień i cytatów zawartych artykułów, aby zapewnić pełne pokrycie artykułów. Ostatecznie zachowano 36 artykułów.

Dwóch badaczy pracowało razem, aby przeprowadzić cały ten proces, a po dyskusji i negocjacjach w celu wyjaśnienia pojawiających się różnic osiągnięto konsensus na poziomie prawie 94,7%.

Kryteria kwalifikacji

Ponieważ nie wszystkie wyszukane badania spełniały kryteria tej metaanalizy, kryteria włączenia i wyłączenia zostały opracowane w następujący sposób:

• Język publikacji włączonych badań był ograniczony do angielskiego i chińskiego, a pełny tekst można było uzyskać. Wykluczono artykuły, które nie odpowiadały językowi publikacji oraz artykuły, które nie zostały opublikowane w latach 2000-2021.
• Projekt badawczy włączonych badań musi być badaniami empirycznymi i ilościowymi, które mogą ocenić wpływ wspólnego rozwiązywania problemów na rozwój krytycznego myślenia. Artykuły, które nie potrafiły zidentyfikować mechanizmów przyczynowych, za pomocą których wspólne rozwiązywanie problemów wpływa na krytyczne myślenie, takie jak artykuły przeglądowe i artykuły teoretyczne, zostały wykluczone.
• Metoda badawcza włączonych badań musi obejmować losowy eksperyment kontrolny, quasi-eksperyment lub naturalny eksperyment, które mają wyższy stopień trafności wewnętrznej z silnymi projektami eksperymentalnymi i mogą w wiarygodny sposób dostarczyć dowodów na to, że krytyczne myślenie i wspólne rozwiązywanie problemów są powiązane przyczynowo. Artykuły zawierające nieeksperymentalne metody badawcze, takie jak badania czysto korelacyjne lub obserwacyjne, zostały wykluczone.
• Uczestnikami włączonych badań byli wyłącznie uczniowie szkół, w tym uczniowie szkół podstawowych i ponadpodstawowych oraz studenci. Artykuły, w których uczestnikami byli uczniowie spoza szkoły, tacy jak pracownicy socjalni lub dorośli słuchacze, zostały wykluczone.
• Wyniki badań włączonych badań muszą zawierać określone znaki, które można wykorzystać do oceny wpływu krytycznego myślenia (np. wielkość próby, wartość średnia lub odchylenie standardowe). Artykuły, które nie posiadały konkretnych wskaźników pomiaru dla krytycznego myślenia i nie mogły obliczyć wielkości efektu, zostały wykluczone.

Projekt kodowania danych

W celu przeprowadzenia metaanalizy konieczne jest zebranie najważniejszych informacji z artykułów, skodyfikowanie właściwości tych informacji oraz przekształcenie danych opisowych w dane ilościowe. Dlatego w tym badaniu zaprojektowano szablon kodowania danych (patrz Tabela 1 ). Ostatecznie zachowano 16 pól kodujących.

Zaprojektowany szablon kodowania danych składał się z trzech informacji. W informacjach opisowych zawarte zostały podstawowe informacje o artykułach: rok wydania, autor, numer seryjny, tytuł artykułu.

Informacje o zmiennych dla projektu eksperymentu miały trzy zmienne: zmienną niezależną (metoda nauczania), zmienną zależną (myślenie krytyczne) i zmienną moderującą (etap uczenia się, rodzaj nauczania, czas trwania interwencji, rusztowanie uczenia się, wielkość grupy, narzędzie pomiarowe, i dziedzina). W zależności od tematu tego badania, strategia interwencji, jako zmienna niezależna, została zakodowana jako wspólne i niewspółpracujące rozwiązywanie problemów. Zmienna zależna, myślenie krytyczne, została zakodowana jako umiejętność poznawcza i skłonność do nastawienia. Siedem zmiennych moderujących utworzono przez zgrupowanie i połączenie eksperymentalnych zmiennych projektowych odkrytych w ramach 36 badań (patrz Tabela 1 ).), gdzie etapy nauki zostały zakodowane jako szkolnictwo wyższe, liceum, gimnazjum i szkoła podstawowa lub niższe; typy nauczania zostały zakodowane jako kursy mieszane, kursy zintegrowane i kursy niezależne; czas trwania interwencji został zakodowany jako 0–1 tygodni, 1–4 tygodni, 4–12 tygodni i więcej niż 12 tygodni; liczebność grup zakodowano jako 2–3 osoby, 4–6 osób, 7–10 osób i więcej niż 10 osób; rusztowania edukacyjne zostały zakodowane jako rusztowanie edukacyjne wspierane przez nauczyciela, rusztowanie edukacyjne wspomagane techniką i rusztowanie edukacyjne wspierane zasobami; narzędzia pomiarowe zostały zakodowane jako standardowe narzędzia pomiarowe (np. WGCTA, CCTT, CCTST i CCTDI) oraz samodostosowujące się narzędzia pomiarowe (np. zmodyfikowane lub wykonane przez badaczy); a obszary tematyczne zostały zakodowane zgodnie z konkretnymi przedmiotami wykorzystanymi w 36 włączonych badaniach.

Informacje o danych zawierały trzy wskaźniki do pomiaru krytycznego myślenia: wielkość próby, wartość średnia i odchylenie standardowe. Należy pamiętać, że badania z różnymi projektami eksperymentalnymi często przyjmują różne wzory do określania wielkości efektu. W tym artykule wykorzystano zaproponowany przez Morrisa wzór obliczania standardowej różnicy średniej (SMD) ( 2008 , s. 369; patrz tabela dodatkowa S3 ).

Procedura wydobywania i kodowania danych

Zgodnie z szablonem kodowania danych (patrz tabela 1 ), informacje o 36 artykułach zostały pobrane przez dwóch badaczy, którzy następnie wprowadzili je do programu Excel (patrz tabela dodatkowa S1 ). Wyniki każdego badania zostały wyodrębnione oddzielnie w procedurze ekstrakcji danych, jeśli artykuł zawierał liczne badania dotyczące krytycznego myślenia lub jeśli badanie oceniało różne wymiary krytycznego myślenia. Na przykład Tiwari i in. ( 2010 ) wykorzystali cztery punkty czasowe, które postrzegano jako liczne różne badania, w celu zbadania wyników krytycznego myślenia, a Chen ( 2013) obejmowało dwie zmienne wynikowe, tj. skłonność do postaw i zdolności poznawcze, które uznano za dwa badania. Po dyskusji i negocjacjach podczas ekstrakcji danych, współczynniki testu spójności dwóch badaczy wyniosły około 93,27%. Tabela uzupełniająca S2wyszczególnia kluczowe cechy 36 uwzględnionych artykułów z 79 wielkościami efektu, w tym informacje opisowe (np. rok wydania, autor, numer seryjny i tytuł artykułu), informacje zmienne (np. zmienne niezależne, zmienne zależne i zmienne moderujące) ) oraz informacje o danych (np. wartości średnie, odchylenia standardowe i wielkość próby). Następnie przeprowadzono testy stronniczości i heterogeniczności publikacji na przykładowych danych za pomocą oprogramowania Rev-Man 5.4, a następnie wyniki testów wykorzystano do przeprowadzenia metaanalizy.

Test stronniczości publikacji

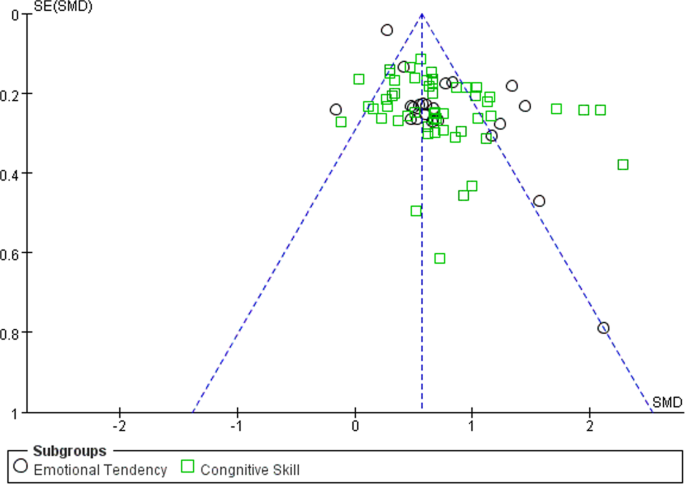
Kiedy próba badań uwzględniona w metaanalizie nie odzwierciedla dokładnie ogólnego stanu badań na dany temat, mówi się, że w tych badaniach występuje stronniczość publikacji. Na wiarygodność i dokładność metaanalizy może mieć wpływ stronniczość publikacji. Z tego powodu metaanaliza musi sprawdzić przykładowe dane pod kątem stronniczości publikacji (Stewart i in., 2006 ). Popularną metodą sprawdzania stronniczości publikacji jest wykres lejkowy; i jest mało prawdopodobne, aby wystąpiła stronniczość publikacji, gdy dane są równomiernie rozproszone po obu stronach średniej wielkości efektu i są ukierunkowane na wyższy region. Dane są równomiernie rozproszone w górnej części strefy efektywnej, zgodnie z wykresem lejkowym związanym z tą analizą (patrz ryc. 2), wskazując, że stronniczość publikacji jest w tej sytuacji mało prawdopodobna.

Ten wykres lejkowy pokazuje wynik błędu publikacji 79 wielkości efektu w 36 badaniach.

Obraz w pełnym rozmiarze

Test heterogeniczności

Aby wybrać odpowiednie modele efektów do metaanalizy, można wykorzystać wyniki testu heterogeniczności wielkości efektów danych. W metaanalizie powszechną praktyką jest mierzenie stopnia heterogeniczności danych za pomocą wartości I ² , przy czym I ²  ≥ 50% jest zazwyczaj rozumiane jako oznaczające średnio-wysoką heterogeniczność, co wymaga przyjęcia modelu efektu losowego; jeśli nie, należy zastosować model z efektem stałym (Lipsey i Wilson, 2001 ). Wyniki testu heterogeniczności w tym artykule (patrz Tabela 2 ) ujawniły, że I2 ^wynosił 86% i wykazywał znaczną heterogeniczność ( P < 0,01). Aby zapewnić dokładność i niezawodność, całkowita wielkość efektu powinna być obliczona z wykorzystaniem modelu efektu losowego.

Analiza ogólnej wielkości efektu

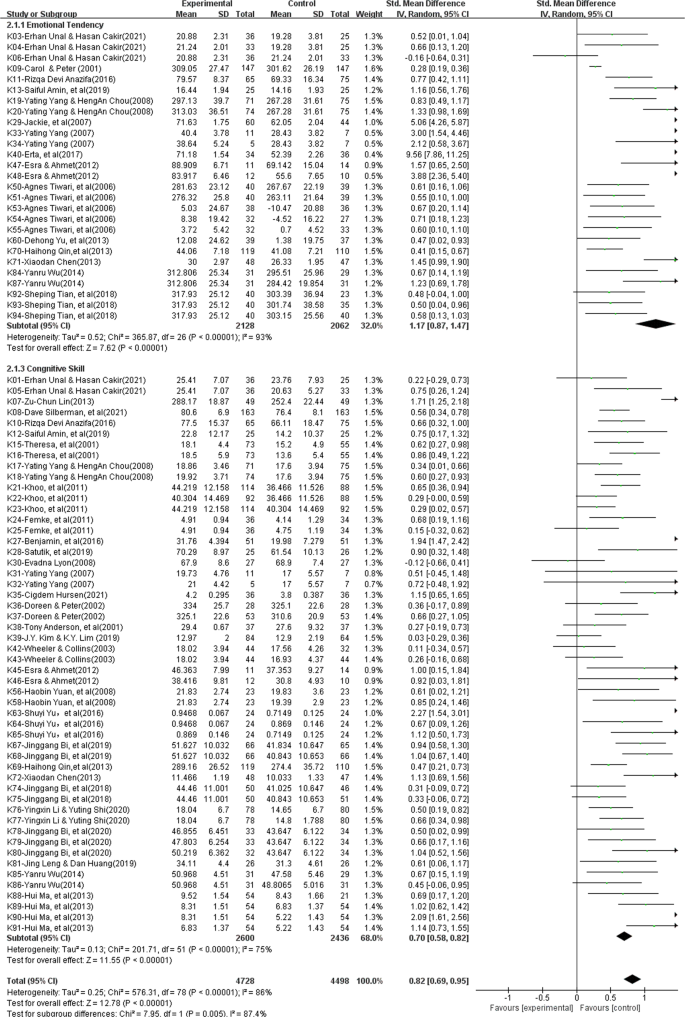
Ta metaanaliza wykorzystała model efektu losowego do zbadania 79 wielkości efektu z 36 badań po wyeliminowaniu heterogeniczności. Zgodnie z kryterium Cohena (Cohen, 1992 ), z wyników analizy, które są pokazane na wykresie leśnym ogólnego efektu (patrz ryc. 3 ), jest całkowicie jasne, że skumulowana wielkość wpływu wspólnego rozwiązywania problemów wynosi 0,82 , co jest istotne statystycznie ( z  = 12,78, P  < 0,01, 95% CI [0,69, 0,95]) i może zachęcić uczących się do ćwiczenia krytycznego myślenia.

Ten wykres lasu pokazuje wynik analizy ogólnej wielkości efektu w 36 badaniach.

Obraz w pełnym rozmiarze

Ponadto w badaniu tym zbadano dwa różne wymiary krytycznego myślenia, aby lepiej zrozumieć dokładny wkład wspólnego rozwiązywania problemów w rozwój krytycznego myślenia. Wyniki (patrz Tabela 3 ) wskazują, że wspólne rozwiązywanie problemów poprawia zdolności poznawcze (ES = 0,70) i ​​skłonność do nastawienia (ES = 1,17), przy znaczących różnicach międzygrupowych (chi ²  = 7,95, P  < 0,01). Chociaż wspólne rozwiązywanie problemów poprawia oba wymiary krytycznego myślenia, należy podkreślić, że poprawa postaw uczniów jest znacznie bardziej wyraźna i ma znaczący kompleksowy efekt (ES = 1,17, z  = 7,62, P < 0,01, 95% CI [0,87, 1,47]), podczas gdy wzrost umiejętności poznawczych uczniów jest nieco lepszy i jest nieco powyżej średniej. (ES = 0,70, z  = 11,55, p  < 0,01, 95% CI [0,58, 0,82]).

Analiza wielkości efektu moderatora

79 wielkości efektu całego poletka leśnego zostało poddanych dwustronnemu testowi, który ujawnił znaczną niejednorodność ( I ²  = 86%, z  = 12,78, P  < 0,01), wskazując różnice między różnymi wielkościami efektu, na które mogły mieć wpływ czynniki moderujące inne niż błąd próbkowania. Dlatego zbadanie możliwych czynników moderujących, które mogą powodować znaczną heterogeniczność, przeprowadzono za pomocą analizy podgrup, takich jak etap uczenia się, rusztowanie uczenia się, typ nauczania, wielkość grupy, czas trwania interwencji, narzędzie pomiarowe i obszar tematyczny zawarty w 36 projektach eksperymentalnych , aby dokładniej zbadać kluczowe czynniki wpływające na krytyczne myślenie. Wyniki (patrz Tabela 4) wskazują, że różne czynniki moderujące mają korzystny wpływ na krytyczne myślenie. W tej sytuacji obszar tematyczny (chi ²  = 13,36, p  < 0,05), wielkość grupy (chi ²  = 8,77, p  < 0,05), czas trwania interwencji (chi ²  = 12,18, p  < 0,01), rusztowanie uczenia się (chi ²  = 9,03, P  < 0,01) i typ nauczania (chi ²  = 7,20, P  < 0,05) są istotnymi moderatorami, które można zastosować do wspierania kultywowania krytycznego myślenia. Ponieważ jednak etap uczenia się i narzędzia pomiarowe nie różniły się istotnie między grupami (chi ²  = 3,15, P = 0,21 > 0,05 i chi ²  = 0,08, P  = 0,78 > 0,05), nie jesteśmy w stanie wyjaśnić, dlaczego te dwa czynniki są kluczowe we wspieraniu kultywowania krytycznego myślenia w kontekście wspólnego rozwiązywania problemów. Oto dokładne wyniki, które przedstawiają się następująco:

Różne etapy uczenia się pozytywnie wpływały na krytyczne myślenie, bez istotnych różnic międzygrupowych (chi ²  = 3,15, P  = 0,21 > 0,05). Na pierwszej liście wielkości efektu znalazło się liceum (ES = 1,36, P  < 0,01), potem wyższe (ES = 0,78, P  < 0,01) i gimnazjum (ES = 0,73, P  < 0,01). Wyniki te pokazują, że pomimo korzystnego wpływu etapu uczenia się na kultywowanie krytycznego myślenia uczniów, nie jesteśmy w stanie wyjaśnić, dlaczego jest on niezbędny do kultywowania krytycznego myślenia w kontekście wspólnego rozwiązywania problemów.

Różne typy nauczania miały różny stopień pozytywnego wpływu na krytyczne myślenie, z istotnymi różnicami międzygrupowymi (chi ²  = 7,20, p  < 0,05). Wielkość efektu oceniono następująco: kursy mieszane (ES = 1,34, p  < 0,01), kursy zintegrowane (ES = 0,81, p  < 0,01) oraz kursy niezależne (ES = 0,27, p  < 0,01). Wyniki te wskazują, że najskuteczniejszym podejściem do kultywowania krytycznego myślenia z wykorzystaniem wspólnego rozwiązywania problemów jest nauczanie na kursach mieszanych.

Różne czasy trwania interwencji znacznie poprawiły krytyczne myślenie i wystąpiły istotne różnice międzygrupowe (chi ²  = 12,18, P  < 0,01). Wielkość efektu związana z tą zmienną wykazywała tendencję wzrostową wraz z dłuższym czasem trwania interwencji. Poprawa krytycznego myślenia osiągnęła znaczący poziom (ES = 0,85, P  < 0,01) po ponad 12 tygodniach treningu. Odkrycia te wskazują, że czas trwania interwencji i wpływ krytycznego myślenia są dodatnio skorelowane, przy czym dłuższy czas trwania interwencji ma większy efekt.

Różne rusztowania (szkielety, schematy, konstrukcje) uczenia się pozytywnie wpłynęły na krytyczne myślenie, z istotnymi różnicami międzygrupowymi (chi ²  = 9,03, P  < 0,01). Rusztowanie uczenia się wspieranego zasobami (ES = 0,69, p  < 0,01) uzyskało średni do wysokiego poziom wpływu, rusztowanie uczenia się wspieranego techniką (ES = 0,63, p  < 0,01) również osiągnęło średni do wysokiego poziomu wpływu, a rusztowanie uczenia się wspieranego przez nauczyciela (ES = 0,92, p  < 0,01) wykazało wysoki poziom znaczącego wpływu. Wyniki te pokazują, że rusztowanie edukacyjne ze wsparciem nauczyciela ma największy wpływ na kultywowanie krytycznego myślenia.

Różne wielkości grup pozytywnie wpływały na krytyczne myślenie, a różnice międzygrupowe były istotne statystycznie (chi ²  = 8,77, p  < 0,05). Myślenie krytyczne wykazywało ogólny trend spadkowy wraz ze wzrostem wielkości grupy. Ogólna wielkość efektu 2–3 osób w tej sytuacji była największa (ES = 0,99, P  < 0,01), a gdy liczebność grupy była większa niż 7 osób, poprawa krytycznego myślenia była na poziomie niższym średnim (ES < 0,5, P  < 0,01). Wyniki te pokazują, że wpływ na krytyczne myślenie jest pozytywnie związany z wielkością grupy, a wraz ze wzrostem liczebności grupy rośnie również ogólny wpływ.

Różne narzędzia pomiarowe pozytywnie wpłynęły na krytyczne myślenie, z istotnymi różnicami międzygrupowymi (chi ²  = 0,08, P  = 0,78 > 0,05). W tej sytuacji samoadaptujące się narzędzia pomiarowe uzyskały średni poziom efektu (ES = 0,78), podczas gdy całkowita wielkość efektu standaryzowanych narzędzi pomiarowych była największa, osiągając istotny poziom efektu (ES = 0,84, P  < 0,01). Wyniki te pokazują, że pomimo korzystnego wpływu narzędzia pomiarowego na kultywowanie krytycznego myślenia, nie jesteśmy w stanie wyjaśnić, dlaczego jest ono kluczowe we wspieraniu rozwoju krytycznego myślenia poprzez wykorzystanie podejścia polegającego na wspólnym rozwiązywaniu problemów.

Różne obszary tematyczne miały większy wpływ na krytyczne myślenie, a różnice międzygrupowe były istotne statystycznie (chi ²  = 13,36, p  < 0,05). Matematyka miała największy ogólny wpływ, osiągając znaczący poziom efektu (ES = 1,68, p  < 0,01), a następnie nauki ścisłe (ES = 1,25, p  < 0,01) i medycyna (ES = 0,87, p  < 0,01). który również osiągnął znaczny poziom efektu. Najmniej skuteczna była technologia programowania (ES = 0,39, p  < 0,01), mając jedynie średnio-niski stopień skuteczności w porównaniu z edukacją (ES = 0,72, p  < 0,01) i innymi dziedzinami (takimi jak język, sztuka i nauki społeczne ) (ES = 0,58, p < 0,01). Wyniki te sugerują, że dziedziny naukowe (np. matematyka, nauki ścisłe) mogą być najskuteczniejszymi obszarami przedmiotowymi do kultywowania krytycznego myślenia z wykorzystaniem podejścia polegającego na wspólnym rozwiązywaniu problemów.

Skuteczność wspólnego rozwiązywania problemów w aspekcie nauczania krytycznego myślenia

Zgodnie z tą metaanalizą, stosowanie wspólnego rozwiązywania problemów jako strategii interwencji w nauczaniu krytycznego myślenia ma znaczny wpływ na kultywowanie krytycznego myślenia uczniów jako całości i ma korzystny wpływ promocyjny na dwa wymiary krytycznego myślenia. Według niektórych badań wspólne rozwiązywanie problemów, najczęściej stosowana strategia nauczania krytycznego myślenia w programie nauczania, może znacznie poprawić krytyczne myślenie uczniów (np. Liang i in., 2017 ; Liu i in., 2020 ; Cindy, 2004). Ta metaanaliza zapewnia zbieżne wsparcie danych dla powyższych poglądów badawczych. Zatem wyniki tej metaanalizy nie tylko skutecznie odnoszą się do pierwszego pytania badawczego dotyczącego ogólnego efektu kultywowania krytycznego myślenia i jego wpływu na dwa wymiary krytycznego myślenia (tj. skłonność do postaw i umiejętności poznawcze), wykorzystując podejście problemu współpracy rozwiązywania problemów, ale także zwiększać naszą pewność siebie w kultywowaniu krytycznego myślenia poprzez zastosowanie podejścia interwencyjnego opartego na współpracy i rozwiązywaniu problemów w kontekście nauczania w klasie.

Co więcej, związana z tym poprawa tendencji do postaw jest znacznie silniejsza, ale odpowiadająca jej poprawa umiejętności poznawczych jest tylko nieznacznie lepsza. Według niektórych badań umiejętności poznawcze różnią się od tendencji do postaw w nauczaniu w klasie; kultywowanie i rozwijanie tej pierwszej jako kluczowej umiejętności jest procesem stopniowej akumulacji, podczas gdy na tę drugą jako postawę wpływa kontekst sytuacji nauczania (np. nowatorskie i ekscytujące podejście do nauczania, ambitne i satysfakcjonujące zadania) (Halpern , 2001 ; Wei i Hong, 2022). Wspólne rozwiązywanie problemów jako podejście do nauczania jest ekscytujące i interesujące, a także satysfakcjonujące i stanowi wyzwanie; ponieważ koncentruje się na uczniach i bada problemy o słabej strukturze w rzeczywistych sytuacjach, i może zainspirować uczniów do pełnego wykorzystania ich potencjału do rozwiązywania problemów, co znacznie poprawi ich skłonność do rozwiązywania problemów (Liu i in., 2020 ). Podobnie jak wspólne rozwiązywanie problemów wpływa na skłonność do nastawienia, tendencja do nastawienia wpływa na umiejętności poznawcze podczas próby rozwiązania problemu (Liu i in., 2020 ; Zhang i in., 2022 ), a silniejsze tendencje nastawienia są związane z lepszymi osiągnięciami w nauce i zdolnościami poznawczymi umiejętności uczniów (Sison, 2008; Zhang i in., 2022 ). Można zauważyć, że wspólne rozwiązywanie problemów ma wpływ na dwa specyficzne wymiary myślenia krytycznego, jak również na myślenie krytyczne jako całość, a niniejsze badanie ukazuje zniuansowane powiązania między umiejętnościami poznawczymi a tendencjami w zakresie postaw w odniesieniu do tych dwóch wymiarów krytycznego myślenia . Aby w pełni rozwinąć zdolność uczniów do krytycznego myślenia, przyszłe badania empiryczne powinny zwracać większą uwagę na umiejętności poznawcze.

Moderujące efekty wspólnego rozwiązywania problemów w odniesieniu do nauczania krytycznego myślenia

Aby dokładniej zbadać kluczowe czynniki wpływające na krytyczne myślenie, zbadano możliwe efekty moderujące, które mogą powodować znaczną heterogeniczność, za pomocą analizy podgrup. Odkrycia pokazują, że czynniki moderujące, takie jak rodzaj nauczania, etap uczenia się, wielkość grupy, rusztowanie uczenia się, czas trwania interwencji, narzędzie pomiarowe i obszar tematyczny uwzględniony w 36 projektach eksperymentalnych, mogą wspierać kultywowanie wspólnego problemu -rozwiązywanie w krytycznym myśleniu. Wśród nich różnice w wielkości efektu między etapem uczenia się a narzędziem pomiarowym nie są znaczące, co nie wyjaśnia, dlaczego te dwa czynniki są kluczowe we wspieraniu kultywowania krytycznego myślenia z wykorzystaniem podejścia polegającego na wspólnym rozwiązywaniu problemów.

Jeśli chodzi o etap uczenia się, różne etapy uczenia się pozytywnie wpłynęły na krytyczne myślenie bez znaczących różnic międzygrupowych, co wskazuje, że nie jesteśmy w stanie wyjaśnić, dlaczego jest to kluczowe we wspieraniu rozwoju krytycznego myślenia.

Chociaż szkolnictwo wyższe stanowi 70,89% wszystkich badań empirycznych przeprowadzonych przez naukowców, szkoła średnia może być odpowiednim etapem nauki, aby wspierać krytyczne myślenie uczniów poprzez wykorzystanie podejścia polegającego na wspólnym rozwiązywaniu problemów, ponieważ ma ono największą ogólną wielkość efektu. Zjawisko to może być związane z rozwojem poznawczym ucznia, co wymaga dalszych badań w dalszych badaniach.

Jeśli chodzi o rodzaj nauczania, nauczanie na kursach mieszanych może być najlepszą metodą nauczania do rozwijania krytycznego myślenia uczniów. Odpowiednie badania wykazały, że w rzeczywistym procesie nauczania, jeśli uczniowie są szkoleni tylko w zakresie metod myślenia, metody, których się uczą, są izolowane i oderwane od wiedzy przedmiotowej, co nie sprzyja ich transferowi metod myślenia; w związku z tym, jeśli myślenie uczniów jest ćwiczone tylko w nauczaniu przedmiotowym bez systematycznego szkolenia metodycznego, trudno jest odnieść je do rzeczywistych warunków (Ruggiero, 2012 ; Hu i Liu, 2015). Nauczanie krytycznego myślenia jako nauczanie na kursie mieszanym, równolegle z nauczaniem innych przedmiotów, może osiągnąć najlepszy efekt w zakresie krytycznego myślenia uczniów, a jawne nauczanie krytycznego myślenia jest bardziej skuteczne niż mniej wyraźne nauczanie krytycznego myślenia (Bensley i Spero, 2014 ).

Jeśli chodzi o czas trwania interwencji, przy dłuższych czasach interwencji, ogólna wielkość efektu wykazuje tendencję wzrostową. Zatem czas trwania interwencji i wpływ krytycznego myślenia są pozytywnie skorelowane. Myślenie krytyczne, jako kluczowa kompetencja uczniów XXI wieku, jest trudne do uzyskania znaczącej poprawy w krótkim czasie trwania interwencji. Zamiast tego można go rozwijać przez długi czas poprzez konsekwentne nauczanie i stopniowe gromadzenie wiedzy (Halpern, 2001 ; Hu i Liu, 2015 ). Dlatego przyszłe badania empiryczne powinny uwzględniać te ograniczenia w dłuższym okresie nauczania krytycznego myślenia.

Jeśli chodzi o wielkość grupy, wielkość grupy 2–3 osób ma największą wielkość efektu, a ogólna wielkość efektu maleje wraz ze wzrostem liczebności grupy. Wynik ten jest zgodny z niektórymi wynikami badań; na przykład grupa złożona z dwóch do czterech członków jest najbardziej odpowiednia do wspólnego uczenia się (Schellens i Valcke, 2006). Jednak wyniki metaanalizy wskazują również, że gdy wielkość grupy przekracza 7 osób, małe grupy nie mogą zapewnić lepszej interakcji i wydajności niż duże grupy. Może to wynikać z faktu, że rusztowania edukacyjne wspierające technikę, wsparcie zasobów i wsparcie nauczyciela poprawiają częstotliwość i efektywność interakcji między członkami grupy, a grupa współpracująca z większą liczbą członków może zwiększyć różnorodność poglądów, co jest pomocne w kultywowaniu krytycznego myślenia z wykorzystaniem podejście polegające na wspólnym rozwiązywaniu problemów.

Jeśli chodzi o rusztowanie uczenia się, wszystkie trzy różne rodzaje rusztowań uczenia się mogą poprawić krytyczne myślenie. Wśród nich rusztowanie uczenia się wspierane przez nauczyciela ma największy ogólny rozmiar efektu, wykazując współzależność skutecznych rusztowań uczenia się i wspólnego rozwiązywania problemów. Wynik ten jest zgodny z niektórymi wynikami badań; na przykład skuteczną strategią jest zachęcanie uczniów do współpracy, szukania rozwiązań i rozwijania umiejętności krytycznego myślenia za pomocą rusztowań edukacyjnych (Reiser, 2004 ; Xu i in., 2022 ); rusztowania edukacyjne mogą zmniejszyć złożoność zadań i nieprzyjemne odczucia, jednocześnie zachęcając uczniów do zaangażowania się w działania edukacyjne (Wood i in., 2006); rusztowania edukacyjne mają na celu pomóc uczniom w skuteczniejszym stosowaniu metod uczenia się w celu dostosowania procesu wspólnego rozwiązywania problemów, a rusztowania edukacyjne wspierane przez nauczyciela mają największy wpływ na krytyczne myślenie w tym procesie, ponieważ są bardziej ukierunkowane, dostarczają informacji i są aktualne ( Xu i in., 2022 ).

W odniesieniu do narzędzia pomiarowego, mimo że wystandaryzowane narzędzia pomiarowe (takie jak WGCTA, CCTT i CCTST) zostały uznane przez światowych ekspertów za godne zaufania i skuteczne, przyjęło je tylko 54,43% badań uwzględnionych w tej metaanalizie do oceny, a wyniki nie wykazały różnic międzygrupowych. Wyniki te sugerują, że nie wszystkie okoliczności nauczania są odpowiednie do pomiaru krytycznego myślenia za pomocą standardowych narzędzi pomiarowych. „Narzędzia pomiarowe do pomiaru zdolności myślenia mają ograniczenia w ocenie uczniów w sytuacjach edukacyjnych i powinny być odpowiednio dostosowane, aby dokładnie ocenić zmiany w krytycznym myśleniu uczniów”, według Simpsona i Courtney ( 2002, p. 91). W rezultacie, aby pełniej i dokładniej ocenić, w jaki sposób ewoluowało krytyczne myślenie uczniów, musimy odpowiednio zmodyfikować standardowe narzędzia pomiarowe oparte na kontekstach uczenia się opartych na wspólnym rozwiązywaniu problemów.

Jeśli chodzi o obszar przedmiotowy, kompleksowy efekt działów nauk ścisłych (np. matematyki, nauk ścisłych, nauk medycznych) jest większy niż w przypadku nauk językowych i społecznych. W niektórych niedawnych międzynarodowych reformach edukacyjnych zauważono, że krytyczne myślenie jest podstawową częścią umiejętności naukowych. Uczniowie posiadający wiedzę naukową mogą udowodnić racjonalność swojej oceny na podstawie dokładnych dowodów i rozsądnych standardów, gdy stają w obliczu wyzwań lub źle ustrukturyzowanych problemów (Kyndt i in., 2013 ), co sprawia, że ​​krytyczne myślenie ma kluczowe znaczenie dla rozwijania wiedzy naukowej i stosowania tej wiedzy w praktyce rozwiązywanie problemów związanych z nauką, technologią i społeczeństwem (Yore i in., 2007 ).

Sugestie dotyczące nauczania krytycznego myślenia

Oprócz tych przedstawionych w powyższej dyskusji, podane są następujące sugestie dotyczące nauczania krytycznego myślenia z wykorzystaniem podejścia polegającego na wspólnym rozwiązywaniu problemów.

Po pierwsze, nauczyciele powinni położyć szczególny nacisk na dwa podstawowe elementy, którymi są współpraca i rozwiązywanie problemów, aby projektować rzeczywiste problemy w oparciu o wspólne sytuacje. Ta metaanaliza dostarcza dowodów na poparcie poglądu, że wspólne rozwiązywanie problemów ma silny synergiczny wpływ na promowanie krytycznego myślenia uczniów. Zadawanie pytań na temat rzeczywistych sytuacji i umożliwianie uczniom wzięcia udziału w krytycznych dyskusjach na temat rzeczywistych problemów podczas zajęć to kluczowe sposoby uczenia krytycznego myślenia, a nie tylko czytania spekulatywnych artykułów bez praktyki (Mulnix, 2012 ). Ponadto poprawa krytycznego myślenia uczniów jest realizowana poprzez konflikt poznawczy z innymi uczniami znajdującymi się w sytuacji problemowej (Yang i in., 2008). W związku z tym ważne jest, aby nauczyciele kładli szczególny nacisk na dwa podstawowe elementy, którymi są współpraca i rozwiązywanie problemów, oraz projektowali rzeczywiste problemy i zachęcali uczniów do dyskusji, negocjowania i argumentowania w oparciu o wspólne rozwiązywanie problemów.

Po drugie, nauczyciele powinni projektować i wdrażać kursy mieszane, aby kultywować krytyczne myślenie uczniów, wykorzystując podejście polegające na wspólnym rozwiązywaniu problemów. Krytycznego myślenia można uczyć poprzez program nauczania (Kuncel, 2011 ; Leng i Lu, 2020), którego celem jest kultywowanie krytycznego myślenia uczniów w celu elastycznego transferu i zastosowania w rzeczywistych sytuacjach rozwiązywania problemów. Ta metaanaliza pokazuje, że nauczanie na kursach mieszanych ma bardzo istotny wpływ na kultywowanie i promowanie krytycznego myślenia uczniów. Dlatego nauczyciele powinni projektować i wdrażać nauczanie na kursach mieszanych z rzeczywistymi sytuacjami wspólnego rozwiązywania problemów w połączeniu z treścią wiedzy z określonych dyscyplin w konwencjonalnym nauczaniu, uczyć metod i strategii krytycznego myślenia w oparciu o słabo ustrukturyzowane problemy, aby pomóc uczniom opanować krytyczne myślenie oraz zapewnić praktyczne zajęcia, w których uczniowie mogą wchodzić w interakcje ze sobą w celu rozwijania konstrukcji wiedzy i krytycznego myślenia z wykorzystaniem podejścia polegającego na wspólnym rozwiązywaniu problemów.

Po trzecie, nauczyciele powinni być lepiej przeszkoleni w zakresie krytycznego myślenia, zwłaszcza nauczyciele przygotowujący się do pracy, a także powinni być świadomi sposobów, w jakie wsparcie nauczycieli dla rusztowań edukacyjnych może promować krytyczne myślenie. Rusztowanie edukacyjne wspierane przez nauczycieli miało największy wpływ na krytyczne myślenie uczniów, a ponadto było bardziej ukierunkowane, ukierunkowane i terminowe (Wood i in., 2006 ). Krytycznego myślenia można skutecznie uczyć tylko wtedy, gdy nauczyciele dostrzegają znaczenie krytycznego myślenia dla rozwoju uczniów i stosują odpowiednie podejście podczas projektowania działań instruktażowych (Forawi, 2016). Dlatego też, mając na celu umożliwienie nauczycielom tworzenia rusztowań edukacyjnych w celu kultywowania krytycznego myślenia uczniów z wykorzystaniem podejścia opartego na wspólnym rozwiązywaniu problemów, konieczne jest skoncentrowanie się na rusztowaniach edukacyjnych wspieranych przez nauczycieli i ulepszenie instrukcji nauczania krytycznego myślenia dla nauczycieli, zwłaszcza nauczyciele przedszkolni.

Implikacje i ograniczenia

Istnieją pewne ograniczenia w tej metaanalizie, ale przyszłe badania mogą je skorygować. Po pierwsze, języki wyszukiwania były ograniczone do angielskiego i chińskiego, więc możliwe jest, że pominięto odpowiednie badania, które zostały napisane w innych językach, co skutkowało niewystarczającą liczbą artykułów do przeglądu. Po drugie, dane zawarte w włączonych badaniach są częściowo niedostępne, np. czy nauczyciele byli przeszkoleni w zakresie teorii i praktyki krytycznego myślenia, średni wiek i płeć uczniów oraz różnice w krytycznym myśleniu wśród uczniów w różnym wieku i różnej płci. Po trzecie, co jest typowe dla artykułów przeglądowych, w trakcie wykonywania tej metaanalizy opublikowano więcej badań; dlatego miał limit czasowy. Wraz z rozwojem odpowiednich badań przyszłe badania koncentrujące się na tych zagadnieniach są bardzo istotne i potrzebne.

Temat wielkości wpływu wspólnego rozwiązywania problemów na wspieranie krytycznego myślenia uczniów, któremu poświęcono niewielką uwagę w innych badaniach, został pomyślnie poruszony w niniejszym badaniu. Kwestia skuteczności wspólnego rozwiązywania problemów w promowaniu krytycznego myślenia uczniów została poruszona w tym badaniu, które dotyczyło tematu, któremu we wcześniejszych badaniach poświęcano niewiele uwagi. Można wyciągnąć następujące wnioski:

Jeśli chodzi o uzyskane wyniki, wspólne rozwiązywanie problemów jest skutecznym podejściem dydaktycznym wspierającym krytyczne myślenie uczniów, ze znaczną ogólną wielkością efektu (ES = 0,82, z  = 12,78, P  < 0,01, 95% CI [0,69, 0,95]). W odniesieniu do wymiarów krytycznego myślenia, wspólne rozwiązywanie problemów może znacząco i skutecznie poprawić tendencje postawowe uczniów, a kompleksowy efekt jest znaczący (ES = 1,17, z  = 7,62, P  < 0,01, 95% CI [0,87, 1,47] ); niemniej jednak nie poprawia umiejętności poznawczych uczniów, mając jedynie wpływ na wyższą średnią (ES = 0,70, z  = 11,55, P  < 0,01, 95% CI [0,58, 0,82]).

Jak wykazały zarówno wyniki, jak i dyskusja, istnieje różny stopień korzystnego wpływu na krytyczne myślenie uczniów ze wszystkich siedmiu czynników moderujących, które stwierdzono w 36 badaniach. W tym kontekście typ nauczania (chi ²  = 7,20, p  < 0,05), czas trwania interwencji (chi ²  = 12,18, p  < 0,01), obszar tematyczny (chi ²  = 13,36, p  < 0,05), wielkość grupy (chi ²  = 8,77, P  < 0,05) oraz rusztowanie uczenia się (chi ²  = 9,03, P < 0,01) wszystkie mają pozytywny wpływ na krytyczne myślenie i można je postrzegać jako ważne czynniki moderujące, które wpływają na rozwój krytycznego myślenia. Ponieważ etap uczenia się (chi ²  = 3,15, P  = 0,21 > 0,05) i narzędzia pomiarowe (chi ²  = 0,08, P  = 0,78 > 0,05) nie wykazały żadnych istotnych różnic międzygrupowych, nie jesteśmy w stanie wyjaśnić, dlaczego te dwa czynniki są kluczowe we wspieraniu kultywowania krytycznego myślenia w kontekście wspólnego rozwiązywania problemów.