Rozkład materii galaktycznej (w tym ciemnej) w przekroju sześciennym Wszechświata. By NASA, ESA, and E. Hallman (University of Colorado, Boulder) – http://www.nasa.gov/mission_pages/hubble/science/hst_img_20080520.html, Public Domain, https://commons.wikimedia.org/w/index.php?curid=7332828
Streszczenie
Zasada Landauera sformułowana w 1961 r. głosi, że logiczna nieodwracalność implikuje fizyczną nieodwracalność i wykazała, że informacja jest fizyczna. Tutaj formułujemy nową zasadę równoważności masy-energii-informacji, proponując, że bit informacji nie jest tylko fizyczny, jak już wykazano, ale ma skończoną i mierzalną masę, podczas gdy przechowuje informacje. W tym kontekście wykazano, że masa bitu informacji w temperaturze pokojowej (300 K) wynosi 3,19 × 10 -38 kg. Aby przetestować hipotezę, proponujemy tutaj eksperyment, przewidujący, że masa urządzenia do przechowywania danych wzrośnie o niewielką wartość, gdy jest pełne informacji cyfrowych w stosunku do jego masy w stanie wymazanym. Dla urządzenia 1 TB szacowana zmiana masy wynosi 2,5 × 10 -25 kg.
I. WSTĘP I TEORIA
Shannon podał matematyczną formułę ilości informacji uzyskanych w wyniku obserwacji wystąpienia zdarzenia w swoim przełomowym artykule z 1948 roku. 1 Ignorując wszelkie szczególne cechy zdarzenia, obserwatora lub metody obserwacji, Shannon opracował swoją teorię, stosując podejście aksjomatyczne, w którym zdefiniował informację (I) uzyskaną w wyniku obserwacji zdarzenia jako funkcję prawdopodobieństwa (p) wystąpienia lub nie wystąpienia zdarzenia, I(p). Drugą własnością aksjomatyczną jest to, że miara informacji jest ciągłą funkcją dodatnią prawdopodobieństwa I(p) ≥ 0. Zdarzenie, które jest pewne, tj. p = 1, nie daje zatem żadnej informacji ze swojego wystąpienia, więc I(1) = 0. Zakładając, że dla n niezależnych zdarzeń o indywidualnych prawdopodobieństwach p i łączne prawdopodobieństwo p jest iloczynem ich indywidualnych prawdopodobieństw, wówczas informacja, którą otrzymujemy z obserwacji zbioru n zdarzeń, jest sumą informacji pojedynczego zdarzenia, I(p) = I(p 1 · p 2 ·…· p n ) = I(p 1 ) + I(p 2 ) + … + I(p n ) . Shannon stwierdził, że jedyną funkcją spełniającą te własności aksjomatyczne jest funkcja logarytmiczna, a dla zdarzenia, którego prawdopodobieństwo wystąpienia wynosi p, informacja wyodrębniona z obserwacji zdarzenia jest następująca:
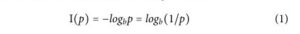
gdzie b jest dowolną bazą, która podaje jednostki informacji, tj. dla bitów informacji binarnej b = 2. Załóżmy zbiór n niezależnych i odrębnych zdarzeń X = {x 1 , x 2 ,…, x n } mający rozkład prawdopodobieństwa P = {p 1 , p 2 , … ,p n } na X , tak że każde zdarzenie x i ma prawdopodobieństwo wystąpienia p i = p(x i ) , gdzie p i ≥ 0 oraz Σp i = 1 . Według Shannona, 1 średnia informacja na zdarzenie, lub liczba bitów informacji na zdarzenie, którą można wyodrębnić, obserwując zbiór zdarzeń X raz, wynosi:
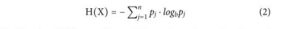
Funkcja H(X) przypomina funkcję entropii informacji i jest maksymalna, gdy zdarzenia x j mają równe prawdopodobieństwa wystąpienia, p j = 1/n , więc H(X) = log b n . Podczas obserwacji N zestawów zdarzeń X lub równoważnie obserwowania N razy zestawu zdarzeń X, liczba bitów informacji wyodrębnionych z obserwacji wynosi N·H(X). Liczba możliwych stanów, znanych również jako odrębne wiadomości w oryginalnym formalizmie Shannona, jest równa liczbie informacji niosących mikrostany, Ω, zgodnych ze stanem makro:
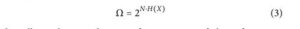
Umożliwia to wprowadzenie entropii stanów niosących informację, wykorzystując entropię termodynamiczną Boltzmanna:
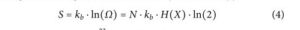
gdzie k b = 1,38064 × 10 -23 J/K jest stałą Boltzmanna.
Przyjrzyjmy się szczególnemu przypadkowi informacji cyfrowej, zakładając b = 2 i dwa możliwe odrębne zdarzenia/stany, więc n = 2 i X = {0,1} . Jeśli założymy brak stronniczości lub pracy zewnętrznej nad systemem, to dwa zdarzenia/stany mają równe prawdopodobieństwo wystąpienia, więc p j = 1/n = 1/2 i p = {p 1 ,p 2 } = {1/2,1/2} , wtedy korzystając ze wzoru (2) można wykazać, że:
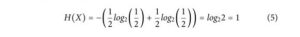
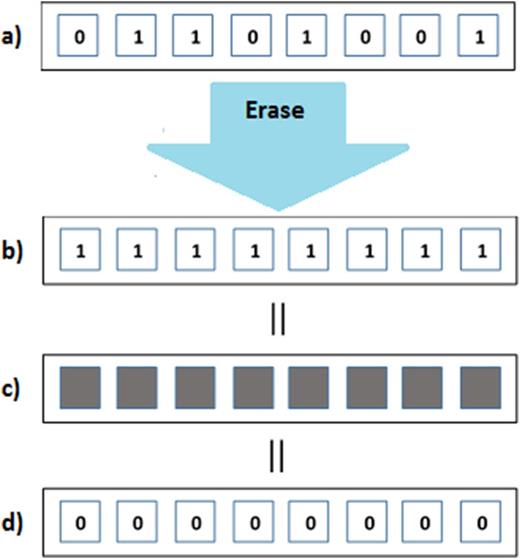
Znaczenie H(X) = 1 jest takie, że 1 bit informacji jest wymagany do zakodowania wiadomości jednoliterowej lub odwrotnie, obserwacja powyższego zdarzenia generuje 1 bit informacji. Używając tego wyniku w (4) otrzymujemy entropię informacyjną jednego bitu S = k b · ln(Ω) = k b · ln(2) . Proces obliczeniowy tworzy informacje cyfrowe za pośrednictwem pewnego rodzaju procesu fizycznego, który podlega prawom fizyki, w tym termodynamice. Stąd musi istnieć bezpośredni związek między procesem tworzenia, manipulowania lub usuwania informacji a termodynamiką. W 1961 roku Landauer po raz pierwszy zaproponował związek między termodynamiką a informacją, postulując, że logiczna nieodwracalność procesu obliczeniowego implikuje fizyczną nieodwracalność. 2 Ponieważ procesy nieodwracalne są rozpraszające, wynika z tego, że logiczna nieodwracalność jest również procesem rozpraszającym, a przez ekstrapolację informacja jest fizyczna. 3 Przykładem logicznego nieodwracalnego procesu jest operacja „kasowania” urządzenia pamięci. Urządzenie pamięci to odrębna skończona tablica N elementów binarnych, która może przechowywać informacje bez rozpraszania. Rozważmy izolowany system fizyczny, który działa jako cyfrowe urządzenie pamięci składające się z tablicy N bitów. Korzystając z (3) możemy obliczyć, że istnieje 2 N możliwych mikrostanów, a początkowa entropia informacji systemu wynosi S i info = Nk b · ln(2). Całkowita entropia systemu składa się z entropii fizycznej, S i phys związanej ze stanami nieniosącymi informacji, oraz entropii informacji, charakterystycznej dla stanów niosących informację. Wykonanie nieodwracalnej operacji logicznej, takiej jak „wymazywanie”, wprowadza system w jeden z trzech równoważnych wymazanych stanów, jak pokazano na rysunku 1 dla tablicy 8 bitów, znanej również jako bajt. Początkowy bajt w tym przykładzie jest losowo wybierany jako 01101001, co reprezentuje literę „i” zakodowaną binarnie ( rys. 1a ). Stan wymazany zdefiniowany przez Landauera jest w rzeczywistości operacją resetowania ze wszystkimi bitami w stanie 1 ( rys. 1b ) lub 0 ( rys. 1d ), ale są one równoważne prawdziwemu stanowi „wymazanemu”, który nie jest ani 0, ani 1, jak na rys. 1c.Przykładem prawdziwego stanu wymazanego byłaby tablica bitów w pamięci magnetycznej, w której operacja wymazywania nie oznacza zresetowania wszystkich bitów do identycznego stanu namagnesowanego, ale całkowite rozmagnesowanie każdego bitu, więc ani 1, ani 0 nie mogłyby zostać zidentyfikowane w żadnym z bitów. Oznacza to, że system ma tylko jeden możliwy stan informacji, n = 1, więc używając (2) otrzymujemy H(X) = 0 i S info (wymazane) = S f info = 0. Zatem operacja „wymazywania” zmniejsza entropię informacji systemu, ΔS info = S f info – S i info = – Nk b · ln2. Ponieważ druga zasada termodynamiki stwierdza, że całkowita zmiana entropii nie może maleć w czasie, ΔS tot = ΔS phys + ΔS info ≥ 0 , wówczas nieodwracalne obliczenia muszą zmniejszyć entropię informacyjną stanów niosących informację poprzez zwiększenie entropii stanów nieniosących informacji poprzez cieplną dyssypację energii, ΔQ/T = ΔS phys ≤ Nk b · ln(2) . W przypadku jednego bitu informacji utraconego nieodwracalnie, entropia układu musi wzrosnąć o wartość bezwzględną ciepła uwalnianego na każdy utracony bit, ΔQ = k b · T · ln(2) , co jest znane jako zasada Landauera. 2,3 Chociaż zasada Landauera była przedmiotem pewnych kontrowersji, obecnie społeczność naukowa szeroko ją akceptuje, a czytelnika odsyłamy do niedawnego eksperymentalnego potwierdzenia zasady Landauera, 4–7, jak również do różnych argumentów teoretycznych na jej poparcie. 8
a) Bajt w losowo zarejestrowanym mikrostanie pamięci; b) Bajt po operacji kasowania resetującej wszystkie bity do stanu 1; c) Bajt po prawdziwej operacji kasowania, w której wszystkie bity nie znajdują się ani w stanie 0, ani 1; d) Bajt po operacji kasowania resetującej wszystkie bity do stanu 0.
II. ROZSZERZONA ZASADA LANDAUERSA
Ustaliliśmy, że proces tworzenia informacji wymaga W ≥ kpracy zewnętrznej b · T · ln(2), aby zmodyfikować układ fizyczny i utworzyć bit informacji, podczas gdy proces usuwania bitu informacji generuje ΔQ ≤ k b · T · ln(2) energii cieplnej uwalnianej do otoczenia, co zostało już określone i potwierdzone eksperymentalnie. 6,7 Jednak gdy raz utworzony zostanie bit informacji, zakładając brak zewnętrznych zaburzeń, może on pozostać taki w nieskończoność bez rozpraszania energii. W tym artykule zaproponowano radykalny pomysł, w którym proces utrzymywania informacji w nieskończoność bez rozpraszania energii można wyjaśnić faktem, że gdy raz utworzony zostanie bit informacji, nabywa on skończoną masę, m bit . Jest to masa równoważna nadmiarowi energii wytworzonej w procesie obniżania entropii informacji, gdy bit informacji jest usuwany. Korzystając z zasady równoważności masy i energii, masa bitu informacji wynosi:
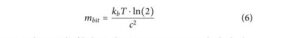
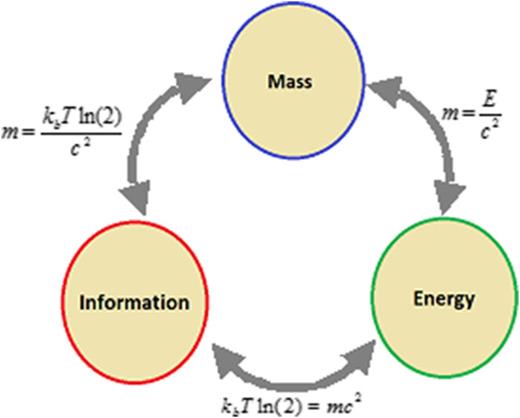
gdzie c jest prędkością światła, a T jest temperaturą, w której przechowywany jest bit informacji. Przechowywanie zawartości informacji w masie fizycznej pozwala na przechowywanie informacji bez rozpraszania energii w nieskończoność. Wymazanie informacji wymaga zewnętrznej pracy wejściowej, a bit masy m jest ponownie przekształcany w energię/ciepło. Implikacje tego rozumowania są takie, że zasada równoważności masy – energii wywnioskowana ze szczególnej teorii względności może być ekstrapolowana do zasady równoważności masy – energii – informacji, jak pokazano na rysunku 2 , który zasadniczo stanowi rozszerzenie oryginalnej zasady Landauera.
Ponadto informacja zależy od temperatury, w której istnieje bit informacji. Z (6) wynika, że m bit = 0 przy T = 0K, więc zgodnie z oczekiwaniami żadna informacja nie może istnieć przy zerowym absolutnym. Korzystając z relacji (6) w temperaturze pokojowej (T = 300K), szacowana masa bitu wynosi ∼ 3,19×10 -38 Kg.
Ważne jest, aby podkreślić, że praca zewnętrzna lub siły przyłożone do dowolnego rodzaju cyfrowych bitów informacji mogą skutkować zaburzeniami stanów pamięci, a nawet samoistnym wymazaniem. W tym artykule ograniczamy podejście do stanów pamięci cyfrowej w stanie równowagi, w danej temperaturze. Wszelkie odchylenia od tych warunków są dozwolone, zakładając, że system jest utrzymywany w stanie równowagi. Jeśli ten stan zostanie naruszony, może nastąpić samoistne wymazanie pamięci, a masa bitu zostanie rozproszona z powrotem w energię cieplną, proporcjonalnie do temperatury, w której występuje to zaburzenie.
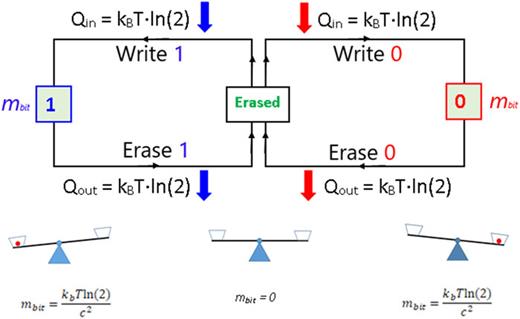
Aby zrozumieć tę koncepcję, wyobraźmy sobie wagę jako urządzenie pamięci (patrz Rysunek 3 ). Gdy waga nie ma przechyłu w lewo ani w prawo, tj. jest w pełni zrównoważona, urządzenie znajduje się w stanie wymazanej pamięci, nie przechowując żadnych informacji. Zgodnie z konwencją, gdy przechyla się w lewo, urządzenie znajduje się w stanie pamięci „1”, a gdy przechyla się w prawo, znajduje się w stanie pamięci „0”. Waga przechyli się tylko wtedy, gdy zostanie wykonana przeciwko niej jakaś praca mechaniczna i zawsze powróci do stanu wymazanego, gdy siła zakłócająca zostanie anulowana. Aby urządzenie mogło przechowywać bit informacji, musi być obecna stała siła/praca. Jednak informacja cyfrowa wymaga początkowej energii wejściowej, aby utworzyć bit, ale następnie jest ona przechowywana w nieskończoność bez rozpraszania energii. Odpowiednikiem tego procesu w kontekście naszego eksperymentu z urządzeniem pamięci wagi myślowej jest sytuacja, gdy wykonywana jest praca zewnętrzna, aby umieścić obiekt o skończonej masie po lewej lub prawej stronie wagi. Jest to proces „zapisu” pamięci. Jednakże obecność masy pozwala na utrzymanie cyfrowego stanu „1” lub „0” w nieskończoność bez rozpraszania energii. Proces wymazywania pamięci jest równoważny pracy zewnętrznej wykonanej w celu usunięcia masy z wagi. W tym procesie masa jest ponownie przekształcana w ciepło, jak opisano w zasadzie Landauera i potwierdzono eksperymentalnie ( Rysunek 3 ).
Cykl energetyczny tworzenia i usuwania bitów cyfrowych wskazujący na energie przenoszone w procesie i równoważną koncepcję w kategoriach równowagi mechanicznej jako urządzenia pamięci. Bit przechowuje informacje bez rozpraszania energii, ponieważ abstrakcyjny bit cyfrowy ma skończoną masę.
Eksperyment myślowy z urządzeniem pamięci równowagi opisany na rysunku 3 pokazuje również cykle energii odpowiadające przejściom ze stanu wymazanego do stanu informacji „1” lub „0” i z powrotem z bitu informacji do stanu wymazanego. Minimalne wejście lub wyjście energii jest wymagane do przejścia bitu do lub ze stanu wymazanego. Jednak po utworzeniu bitu informacji przejścia z „1” do „0” i odwrotnie mogą mieć miejsce bez rozpraszania związanego z tym procesem. Jest to równoważne przesunięciu masy z lewej strony wagi na prawą, bezpośrednio, bez przechodzenia przez stan wymazany.
Proponowana tutaj zasada równoważności masy – energii – informacji jest ściśle stosowalna tylko do klasycznych stanów pamięci cyfrowej w stanie równowagi. Informacje przenoszone przez media relatywistyczne, fale ruchome lub fotony wymagają podejścia teorii informacji relatywistycznej kwantowej i wykraczają poza ramy stosowalności tego artykułu. Podobnie inne formy informacji, w tym informacje analogowe lub informacje osadzone w biologicznych systemach żywych, takich jak DNA, nie są objęte zakresem tej pracy.
III. PROPONOWANY EKSPERYMENT
Poniżej proponujemy prosty eksperyment pozwalający sprawdzić tę teorię poprzez fizyczny pomiar masy informacji cyfrowej.
Polega ona na ultradokładnym pomiarze masy cyfrowego urządzenia do przechowywania danych, gdy wszystkie bity pamięci są w stanie całkowicie wymazanym. Następnie następuje operacja rejestrowania danych cyfrowych na wszystkich bitach pamięci, aż do osiągnięcia pełnej pojemności, po której następuje kolejny dokładny pomiar masy. Jeśli proponowana zasada równoważności masy – energii – informacji jest poprawna, wówczas urządzenie do przechowywania danych powinno być cięższe, gdy przechowywane są na nim informacje, niż gdy jest w stanie całkowicie wymazanym. Można łatwo oszacować różnicę mas, Δm w tym eksperymencie. Załóżmy, że urządzenie pamięci ma pojemność 1 TB, wówczas całkowita liczba bitów pamięci wynosi 10 12 bajtów = 8×10 12 bitów, ponieważ 1 bajt = 8 bitów. Stąd przewidywana zmiana masy w tym eksperymencie wynosi Δm = 2,5×10 -25 kg. Proponowany eksperyment jest prosty pod względem złożoności fizycznej, ale ogólnie bardzo wymagający, ponieważ sukces zależy od umiejętności dokładnego pomiaru zmian masy rzędu ∼10 -25 kg. Wymagana czułość pomiaru może zostać zmniejszona o współczynnik f, jeśli ilość testowanych danych zostanie zwiększona z 1 Tb do f × 1 Tb . Ponieważ pomiar nie jest w rzeczywistości masą bezwzględną, ale raczej zmianą masy Δm, jedną z opcji pomiaru byłby czuły interferometr podobny do Laser Interferometer Gravitational-Wave Observatory (LIGO), 9 chociaż mniejsze rozmiary i czułości byłyby prawdopodobnie wystarczające do proponowanego pomiaru. Inną możliwą opcją przetestowania proponowanej zasady mogłoby być użycie ultraczułej wagi Kibble’a używanej do definiowania kilograma, takiej jak ta opracowana w NPL w Wielkiej Brytanii, 10 chociaż obecne zgłaszane niepewności ∼ 10 -9 są dalekie od wymagań proponowanego eksperymentu.
IV. WNIOSEK
W tym liście zasada Landauera jest ekstrapolowana na zasadę równoważności masy – energii – informacji, poprzez dostarczanie przekonujących argumentów, że fizyczna natura informacji cyfrowej wymaga, aby trochę informacji miało bardzo małą, różną od zera masę. Jest to bardzo abstrakcyjna koncepcja z pewnymi aspektami spekulatywnymi, ale ma zaletę weryfikowalności w środowisku laboratoryjnym, a możliwy eksperyment w celu potwierdzenia proponowanego pomysłu jest opisany w tym liście. Eksperyment jest możliwy do osiągnięcia, a udany test oferowałby bezpośrednie potwierdzenie eksperymentalne zasady równoważności masy – energii – informacji z daleko idącymi implikacjami w fizyce, kosmologii, dużych zbiorach danych, obliczeniach i technologiach. W ramach koncepcji cyfrowego wszechświata cała materia barionowa ma powiązaną zawartość informacyjną. 11 Szacowana masa bitu informacji przy T = 2,73 K wynosi m bitów = 2,91 × 10 -40 Kg. Zakładając, że cała brakująca ciemna materia jest w rzeczywistości masą informacyjną, wstępne szacunki (które zostaną przedstawione w innym artykule) wskazują, że ∼10 93 bitów wystarczyłoby do wyjaśnienia całej brakującej ciemnej materii w widzialnym Wszechświecie. Co ciekawe, liczba ta jest dość bliska innemu szacunkowi zawartości bitów informacyjnych Wszechświata wynoszącej ∼10 87 podanej przez Gougha w 2008 r. za pomocą innego podejścia. 12 W rzeczywistości można by argumentować, że informacja jest odrębną formą materii lub 5. stanem , obok pozostałych czterech obserwowalnych stanów materii stałej, ciekłej, gazowej i plazmowej. Oczekuje się, że praca ta pobudzi dalsze badania teoretyczne i eksperymentalne, przybliżając społeczność naukową o krok do zrozumienia abstrakcyjnej natury materii, energii i informacji we Wszechświecie.
PODZIĘKOWANIE
Praca ta została zainspirowana podczas prowadzenia badań nad ściśle powiązanym grantem badawczym na temat przechowywania danych cyfrowych, finansowanym przez EPSRC (EP/R028656/1). Autor chciałby podziękować za wsparcie otrzymane od School of Mathematics and Physics, University of Portsmouth, na przeprowadzenie tych badań.
1 C. E. Shannon, “A mathematical theory of communication,” The Bell System
Technical Journal 27, 379–423 (1948).
2 R. Landauer, “Irreversibility and heat generation in the computing process,” IBM
Journal of Research and Development 5(3), 183–191 (1961).
3 R. Landauer, “The physical nature of information,” Phys. Lett. A 217(4-5),
188–193 (1996).
4 J. Hong, B. Lambson, S. Dhuey, and J. Bokor, “Experimental test of Landauer’s principle in single-bit operations on nanomagnetic memory bits,” Science
Advances 2(3), e1501492 (2016).
5 G. Rocco, B. Enrique, M. Satoru, H. van der Zant, and L. Fernando, “Quantum Landauer erasure with a molecular nanomagnet,” Nature Physics 14, 565–568
(2018).
6 A. Bérut, A. Arakelyan, A. Petrosyan, S. Ciliberto, R. Dillenschneider, and
E. Lutz, “Experimental verification of Landauer’s principle linking information
and thermodynamics,” Nature 483, 187–189 (2012).
7 Y. Jun, M. Gavrilov, and J. Bechhoefer, “High-precision test of Landauer’s
principle in a feedback trap,” Physical Review Letters 113(19), 190601 (2014).
8 J. Ladyman, S. Presnell, A. J. Short, and B. Groisman, “The connection between
logical and thermodynamic irreversibility,” Studies in History and Philosophy of
Science Part B: Studies in History and Philosophy of Modern Physics 38(1), 58–79
(2007).
9 C. B. Barish and R. Weiss, “LIGO and the detection of gravitational waves,”
Physics Today 52(10), 44 (1999).
10 I. A. Robinson and S. Schlamminger, “The watt or Kibble balance: A technique
for implementing the new SI definition of the unit of mass,” Metrologia 53(5),
A46–A74 (2016).
11 J. D. Bekenstein, “Black holes and information theory,” Contemporary Physics
45(1), 31–43 (2004).
12 M. P. Gough, “Information equation of state,” Entropy 10, 150–159 (2008)
12.
, „
,,
,
–
(
).