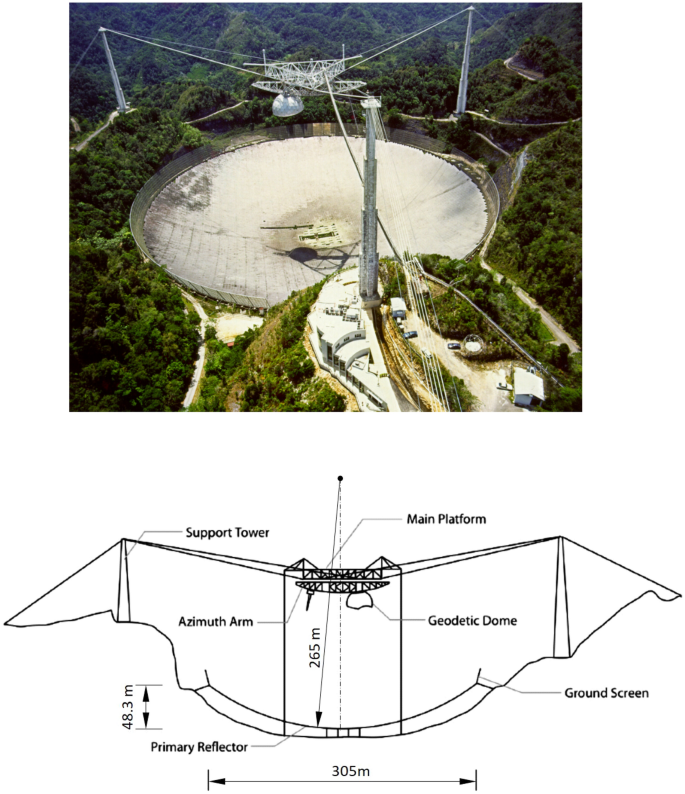
Sferyczny radioteleskop w Arecibo, Obserwatorium Arecibo, Portoryko. Z Wikimedia Commons, repozytorium wolnych multimediów.
Abstrakt
Po wprowadzeniu poprzedników Leonarda da Vinci (LdV) w dziedzinie badań propagacji światła, dokonano analizy jego rysunków na temat odbijania światła przez zwierciadło sferyczne. Przedstawiono odkrycie LdV, zgodnie z którym przy nieskończenie odległym źródle promieni wystarczy mały fragment czaszy, aby wygenerować ognisko, podczas gdy reszta zwierciadła tworzy kaustykę, dla której LdV nie wskazał zastosowania. Podano analityczny opis koncentracji energii w ognisku i na kaustyce wraz z odniesieniem do geometrycznej reprezentacji pola akustycznego w pomieszczeniach. Opierając się na ogólnych zasadach ruchu falowego, przedstawiono symetrię w opisie relacji energetycznych w akustyce i elektromagnetyzmie. Wyjaśniono, dlaczego w polu dźwiękowym w istniejących salach zamiast całej kaustyki obserwuje się tylko jej wierzchołek, który odbierany jest jako punktowe skupienie dźwięku. Określa się wielkość apertury zwierciadła, pokazaną graficznie przez LdV. Pokazano również, w jaki sposób rozwój technik odbiorczych zwiększył aperturę zwierciadła w porównaniu z oszacowaniem LdV. Wdrożenie tych ulepszeń przedstawiono na przykładzie radioteleskopów Arecibo i FAST.
Wstęp
Wczesne rozważania na temat propagacji światła leżą u początków dyscypliny badawczej, która rozwinęła się w dzisiejszą fizykę. Jedną z najwcześniejszych relacji na temat optyki, czyli użycia instrumentów zakłócających bieg światła, jest opowieść z czasów starożytnych o podpaleniu przez Archimedesa rzymskich statków oblegających Syrakuzy za pomocą luster odbijających światło słoneczne [ 1 ] . Kolejnym znaczącym dziełem okresu starożytności, dotyczącym badań optyki, jest późniejszy traktat Ptolemeusza z II w. n.e. [ 2 ]. Zapoczątkowane przez niego rozważania naukowe były kontynuowane w średniowieczu w świecie islamskim. Leonardo da Vinci (LdV) realizował swoje prace w nawiązaniu do tej tradycji [ 3]. Szczególną uwagę poświęcił zastosowaniu zasad optyki geometrycznej w architekturze, malarstwie i grafice, w tym studiach z zakresu perspektywy i światłocienia.
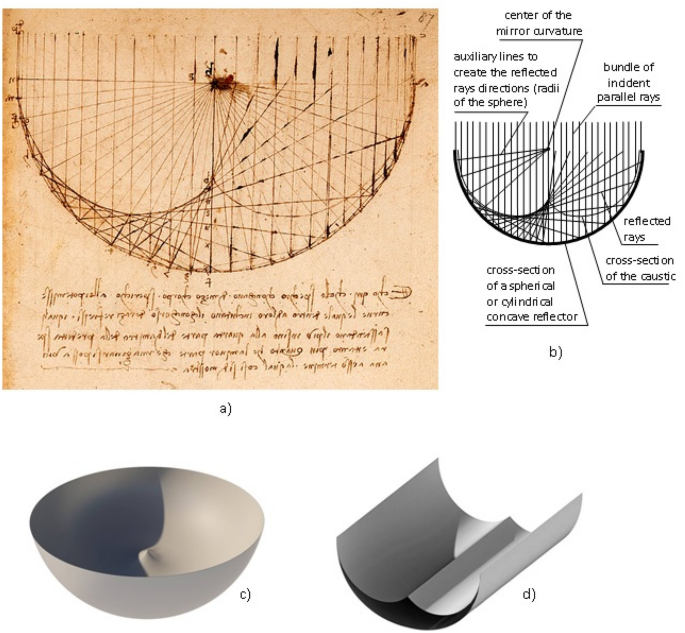
Szkice Leonarda dotyczące optyki zawierają badania nad szczególną formą skupiania promieni świetlnych, zwaną obecnie kaustyką (ryc. 1) .). W konwencji optyki geometrycznej kaustyka to powierzchnia utworzona przez styczne do niej promienie po odbiciu od powierzchni wklęsłej lub w wyniku propagacji w ośrodku niejednorodnym. W pewnych okolicznościach na ługach może tworzyć się guzek. W matematycznym opisie kaustyki odpowiada osobliwości, tzn. parametry pola promieni w tym punkcie dążą do nieskończoności. Fizycznym odpowiednikiem żrącego wierzchołka jest ognisko lustra. Ognisko może również powstać bez towarzyszącej mu substancji żrącej, ale dotyczy to tylko kilku szczególnych przypadków, wśród nich źródła w środku odbłyśnika sferycznego, odbłyśnika parabolicznego z nieskończenie odległym źródłem na swojej osi geometrycznej lub odbłyśnika elipsoidalnego ze źródłem w jednym z ognisk.
Rysunek żrący z notatnika Leonarda da Vinci. Notatka pod rysunkiem na ryc. 1 a, sporządzona słynnym odwróconym pismem Leonarda, mówi, że w zwierciadłach wklęsłych o jednakowej średnicy to, które ma płytszą krzywiznę, skupi największą liczbę odbitych promieni w ognisku i „jak w konsekwencji roznieci ogień z większą szybkością i siłą” [ 9 ] © British Library Board, Źródło: Arundel MS 263. b Szczegóły rysunku Leonarda, ( c , d ) Widoki 3D kaustyki utworzone przez sferyczne i cylindryczne wklęsłe lustra [ 10 ]
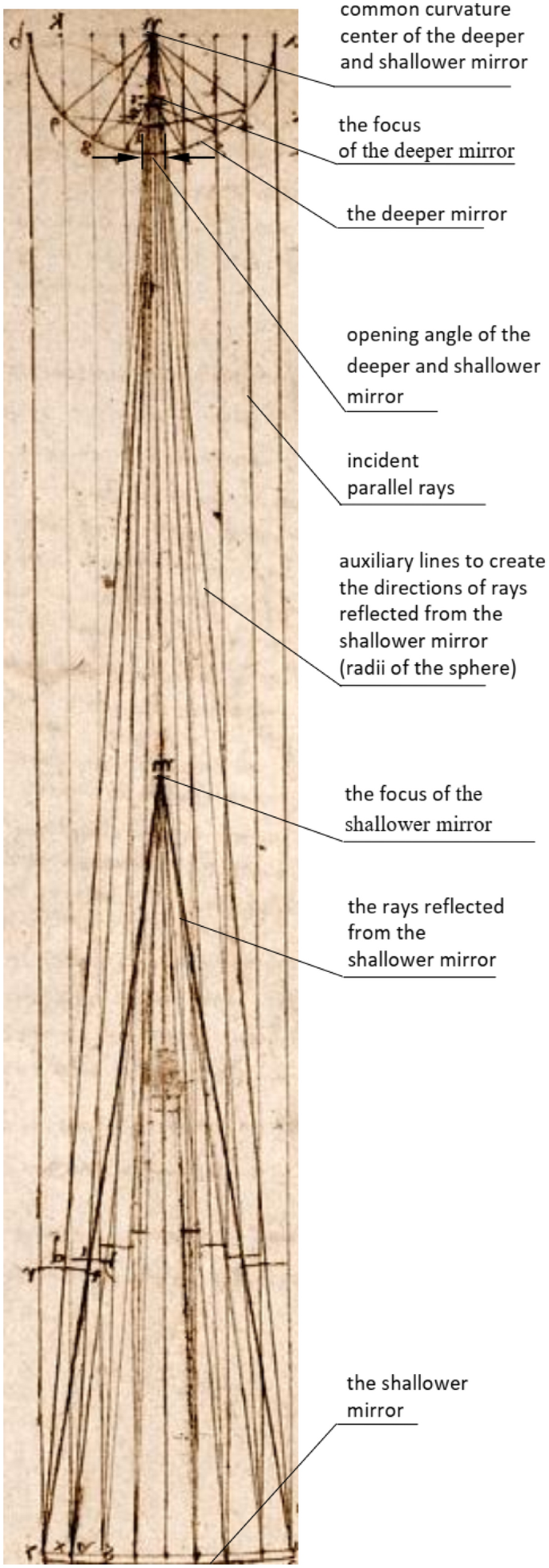
Leonardo wykazał, że przy nieskończenie odległym źródle światła tylko niewielka część sferycznego zwierciadła bierze udział w tworzeniu ogniska. Pozostała część zwierciadła tworzy tylko substancje żrące i jest bezużyteczna dla tworzenia ognisk, co prowadzi do ważnych wniosków praktycznych. Pomysł skupiania światła w ten sposób przypisuje się Archimedesowi, który żył wiele wieków wcześniej, ale analiza ilościowa przedstawiona graficznie na ryc. 2 jest osobistym wkładem Leonarda w badanie zasady działania zwierciadła wklęsłego.
Ilustracja koncepcji Leonarda, w której płytsze zwierciadło (dół) skupia większą liczbę promieni niż zwierciadło z głębszą czaszą o tej samej średnicy (góra) [ 9 ] . © British Library Board, Źródło: Arundel MS 263
Na tym tle historycznym w artykule omówiono powstawanie ognisk i kaustyk w polu akustycznym i elektromagnetycznym. Obserwacje akustyki pomieszczeń wskazują, że w słyszalnym zakresie częstotliwości kaustyka jest tak rozmyta przez dźwięk rozproszony, odbicia fal i interferencję, że zostaje zredukowana do osobliwości. Obserwowana postać kaustyki jest wówczas zwartym obszarem podwyższonego ciśnienia akustycznego o wielkości zależnej od długości fali, co jest wynikiem dyfrakcyjnego poszerzenia ogniska punktowego znanego z analizy graficznej. Dzieje się tak, gdy długość fali jest tego samego rzędu lub nieco krótsza niż długość fali obiektów w polu akustycznym, co jest typowe dla pomieszczeń.
Kiedy długość fali jest znacznie krótsza niż obiekty w polu falowym, efekt rozmycia jest znacznie mniejszy, a substancja kaustyczna działa jak wyraźnie zidentyfikowany obszar skupienia energii. Powstałe w ten sposób kaustyki są obecne w wielu dziedzinach techniki i nauki związanych z rozchodzeniem się światła, ultradźwięków i fal elektromagnetycznych, np. hydroakustyka, aeroakustyka, technika laserowa, a nawet radioastronomia [4 , 5 , 6 ] .
Opierając się na inspiracji rysunkami kaustycznymi w pracach LdV i jego rozważaniach na temat odbijania światła przez zwierciadło wklęsłe, artykuł przedstawia matematyczny opis efektu skupiania promieni. Na tym tle przedstawiono zjawiska zachodzące na kaustykach w polach akustycznych i elektromagnetycznych, uwzględniając ich falowy charakter.
Głównym celem niniejszej pracy jest zbadanie, w jakim stopniu obserwacje LdV dotyczące powstawania kaustyki i ognisk są obecne we współczesnej technice. Artykuł pokazuje, jak szacunki LdV dotyczące apertury lustra rozszerzyły się wraz z rozwojem technik odbioru fal radiowych. O obecności myśli Leonarda w tych działaniach świadczy przykład wielkich radioteleskopów w Arecibo (Portoryko) i Dawodang (Chiny).
Kaustyka w spuściźnie Leonarda da Vinci
Rysunki kaustyki w notatkach Leonarda da Vinci nawiązują do jego badań w dziedzinie optyki w latach 1510–1515 [ 7 , 8 ]. Można w nich znaleźć wiele szkiców ługów na różnych etapach ich powstawania, najbardziej kompletny rysunek ługu przedstawiono na ryc. 1 . Leonardo wykonał swój rysunek 500 lat temu z taką kompetencją, że w artykule jest on cytowany jako doskonale poprawny przykład zastosowania zasad optyki geometrycznej w tworzeniu kaustyki.
Leonardo interesował się potencjalną użytecznością zwierciadeł wklęsłych jako źródeł ciepła, a celem jego badań była ocena właściwości skupiających zwierciadła sferycznego. Rysunek 2 pokazuje dwa lustra różniące się głębokością czaszy, o której mowa w jego odwrotnym skrypcie na ryc. 1a . W swoich późniejszych pracach Leonardo również planował wykorzystać efekt skupienia światła słonecznego do ogrzania, a nawet zagotowania wody [ 11 ].
W świetle dzisiejszego poziomu wiedzy koncepcja Leonarda jest oczywista. Żył jednak 500 lat temu i trafność jego wyjaśnień należy uznać za godną podziwu. Dalsza część artykułu pokazuje, że nawet w tak odległych od optyki dziedzinach, jak akustyka pomieszczeń czy radioastronomia, można odnaleźć koncepcję Leonarda da Vinci.
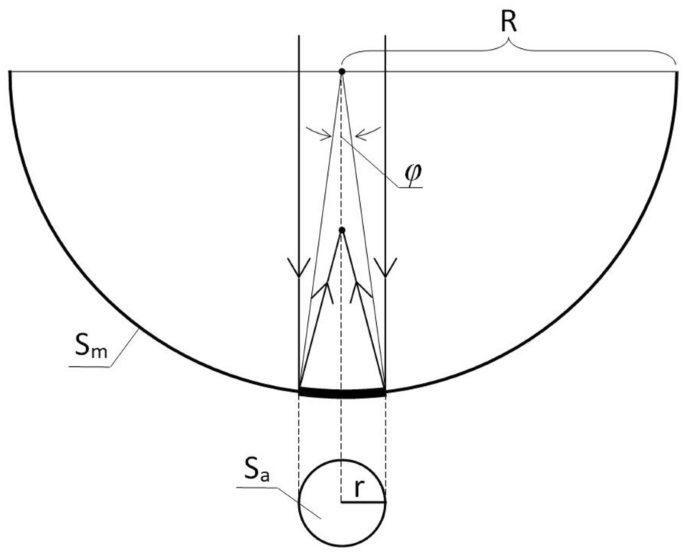
Zgodnie ze współczesną terminologią techniczną ułamek całkowitej energii padającej na zwierciadło, który jest dostępny w odbiorniku, nazywany jest aperturą zwierciadła. Na potrzeby niniejszego artykułu za względną miarę apertury przyjęto stosunek tego pola do pola pełnego zwierciadła półkulistego. Zakładając, że propagacja i odbicie promieni są bezstratne, względna apertura dolnego zwierciadła pokazanego na fig. 2 wynosi około 0,4% (Równania 1 , 2 ).
Dla kąta otwarcia φ = 10° (rys. 3 ) długość łuku r wynosi
a apertura w stosunku do powierzchni pełnego zwierciadła półkulistego wynosi
Analityczny opis koncentracji energii na ługu
Szkice LdV przedstawiają w formie graficznej wpływ koncentracji energii na substancję żrącą. Ta sekcja zawiera ilościową ocenę tego efektu w formie analitycznej, przy użyciu oryginalnego rysunku LdV.
Rozważmy promienie pochodzące z nieskończenie odległego źródła i padające na zwierciadło półkuliste jako wiązkę skolimowaną (ryc. 1a ). Po odbiciu promienie tworzą substancję żrącą opisaną równaniem. ( 3 ) [ 12 ].
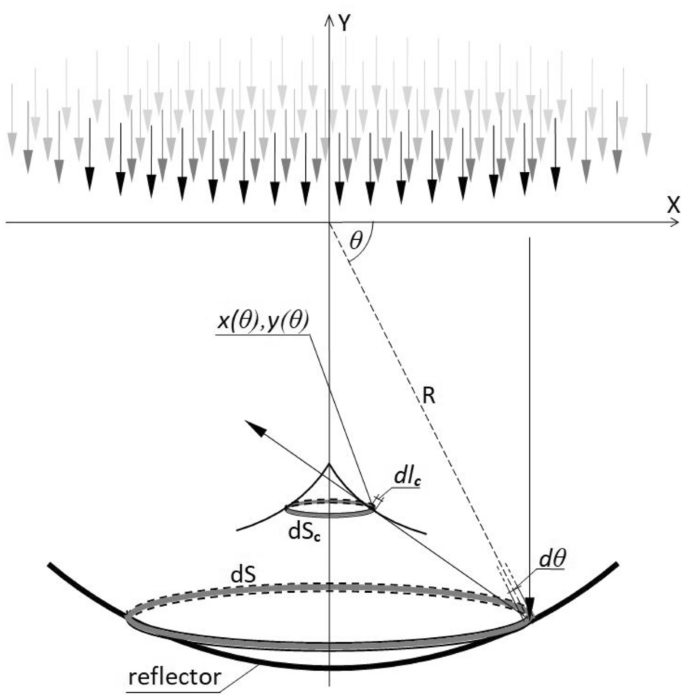
Aby obliczyć gęstość promieni na ługu rozpatrzmy dwa pierścienie wewnątrz czaszy reflektora: dS na jego powierzchni i dSc na ługu (Rys. 4 ) [ 12 , 13 ]. Ponieważ wszystkie promienie odbite od dS są styczne do dS c , względna gęstość promieni na dS c wynosi dS/dS c , gdzie dS i dS c to powierzchnie pierścieni.
Obwód i szerokość pierścienia dS wynoszą 2ΠRcos( θ ) i Rsin( θ )d θ , więc
Podobnie obwód i szerokość pierścienia dS c wynoszą 2Π x ( θ ) i dl c , więc
gdzie dl c jest elementem odcinka żrącego
a pochodne po θ z x(θ), y(θ) to
Elementarna transformacja daje
Podstawienie równania ( 7 ) do Równ. ( 6 ) plony
Więc
Wreszcie, jeśli promienie padające na zwierciadło są rozłożone równomiernie na płaszczyźnie y = 0 (rys. 4 ), względna gęstość promieni C (θ) nad kaustyką wynosi
Ponieważ θ dąży do 0,5Π, C (θ) dąży do nieskończoności, co odpowiada tworzeniu wierzchołków na ługu (ryc. 4 ). Ta osobliwość wynika z kaustycznego pola przekroju poprzecznego dS c dążącego do zera.
Oznaczmy gęstość powierzchniową promieni padających na reflektor jako I o [W/m 2 ]. Gęstość promieni C(θ ) w równaniu. ( 11 ) pomnożone przez Io można zinterpretować jako powierzchniową gęstość energii nad kaustyką w jednostce czasu, czyli natężenie promieni [W/m 2 ].
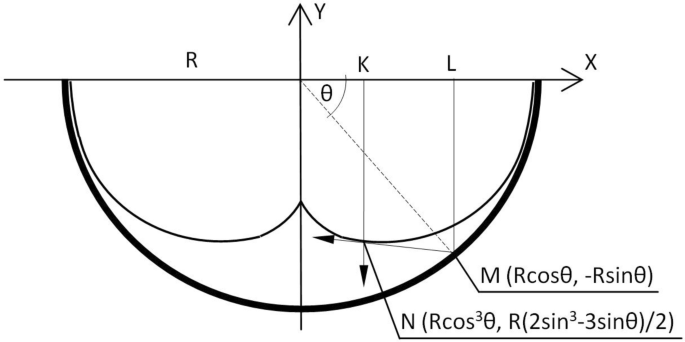
Równanie ( 11 ) pokazuje powierzchniową gęstość mocy na powierzchni ługu. Jest to wartość skończona, z wyjątkiem wierzchołka żrącego, gdzie C (θ) dąży do nieskończoności. Jednakże, gdy rozważymy gęstość energii na płaszczyźnie przekroju żrącego, otrzymamy inny wynik. Na przykład, podążając linią przerywaną od punktu M w kierunku początku układu współrzędnych XY (ryc. 6 ), powierzchniowa gęstość mocy wzrasta i osiąga nieskończoność przy kaustyce. W tym przypadku osobliwość dotyczy całej kaustyki [ 6 ]. W artykule przyjęto jednak analizę powierzchniowej gęstości mocy nie na przekroju ługu, ale na jego powierzchni.
Gdy weźmie się pod uwagę współczynnik absorpcji α odbłyśnika, gdzie α = 0 i α = 1 odnoszą się odpowiednio do całkowitego odbicia i całkowitej absorpcji, względna intensywność promieni wynosi
Na całkowite natężenie promieni nad żrącym I c,res (θ) składa się energia promieni padających I o oraz energia promieni odbitych od żrącego.
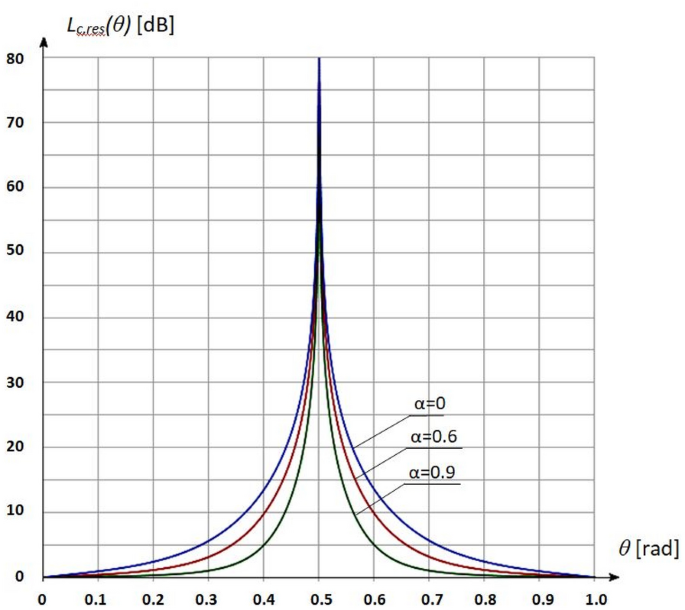
Poziom natężenia promieni na żrącym, przy Io jako natężeniu odniesienia, wynosi wtedy Lc ,res (θ) (rys. 5 ).
Poziom natężenia promieni L c,res (θ) [dB] na kaustyce. współczynnik absorpcji α odbłyśnika [ 12 ]
Kaustyka w polu falowym
Koncepcja ługów LdV i jej rozwój, jak pokazano na rys. 2 i „Analityczny opis koncentracji energii w ługu”, opierają się na podejściu geometrycznym. Mimo odległych w czasie korzeni podejście to jest w pełni funkcjonalnym modelem propagacji energii, stosowanym obecnie np. w akustyce pomieszczeń, optyce czy komunikacji radiowej. W tym rozdziale opisano powstawanie kaustyki w polu falowym, której przejawem jest interferencja padającej fali z falą odbitą od zwierciadła.
Rozważmy falę płaską o długości fali λ znacznie mniejszą od średnicy reflektora D, padającą na reflektor [ 12 ]. W momencie t = 0 czoło fali leży w płaszczyźnie y = 0 (rys. 6 ). Rozchodząc się w głąb reflektora, fala interferuje z falą odbitą, tworząc szereg prążków interferencyjnych wypełniających czaszę lustra i przestrzeń przed nim. Falowy charakter pola jest również przyczyną odchylania fali na krawędzi zwierciadła [ 12 ]. Artykuł dotyczy kaustyki przedstawionej przez LdV, dlatego niniejszy rozdział ograniczono do opisu efektu, który występuje tylko w samej kaustyce, czyli interferencji fali padającej i odbitej.
Kierunki fali padającej i odbitej KN i LMN nakładają się na kaustykę [ 12 ]. Wynik jest sumą ciśnień akustycznych. R: promień odbłyśnika
Zgodnie z prawem odbicia, odbita fala jest styczna do żrącego. Odległości SKN i SLMN przebyte przez falę padającą i odbitą wynoszą
Pomimo zasadniczo różnej natury fal akustycznych i elektromagnetycznych, ogólne zasady ruchu fal opisują zależności energetyczne fal akustycznych i elektromagnetycznych za pomocą tych samych równań, różniących się jedynie fizyczną interpretacją poszczególnych składowych. Istotna różnica dotyczy superpozycji fal, która ma charakter skalarny lub wektorowy odpowiednio dla fal akustycznych lub elektromagnetycznych. W celu ułatwienia porównania równań energetycznych dla obu typów pól przedstawiono je obok siebie.
Natężenie dźwięku I s i powierzchniowa gęstość mocy pola elektromagnetycznego I e , oba w [W/m 2 ], są proporcjonalne do kwadratu ciśnienia akustycznego p 2 [Pascal] i kwadratu amplitudy pola elektrycznego E [V/m] odpowiednio
gdzie ρ: gęstość ośrodka, [kg/m 3 ], c s : prędkość dźwięku (w powietrzu przy ciśnieniu atmosferycznym i temperaturze 15 ° C, c s = 331 m/s, ρc s = 415 [kg /(m 2 s)]), μ o : przepuszczalność próżni (μ o = 4Π10 −7 , [H/m]), c l : prędkość światła (c l = 3*10 8 [m/s]).
Tak więc amplitudy odpowiednio p c ( θ ) i E c ( θ ) ciśnienia akustycznego i pola elektrycznego na ługu wynoszą
gdzie I c,s (θ): natężenie dźwięku na kaustyce, [W/m 2 ], I c,e (θ): gęstość mocy powierzchniowej pola elektromagnetycznego na kaustyce, [W/m 2 ], I o : natężenie padającego dźwięku, [W/m 2 ], I e : gęstość mocy powierzchniowej fali padającej, pole elektromagnetyczne, [W/m 2 ]. α: współczynnik pochłaniania dźwięku, R: współczynnik odbicia składowej elektrycznej fali elektromagnetycznej.
IabsIabs , : intensywność pochłoniętego i padająca fala akustyczna, , : amplituda ciśnienia akustycznego padającej i pochłanianej fali akustycznej, uśredniona dla sferycznego kąta 2Π steradianów. , : amplituda padającego i odbitego pola elektrycznego, uśredniona pod kątem sferycznym 2Π steradianów. Dla uproszczenia w artykule przyjęto całkowite odbicie fali elektromagnetycznej, czyli R = 1.IIIIP¯¯¯IP¯IP¯¯¯absP¯absmi¯¯¯¯Imi¯Imi¯¯¯¯r e flmi¯�mi��
W punkcie czasowym t ciśnienie akustyczne p (t) i amplituda pola elektrycznego odpowiednio padającej fali akustycznej i elektromagnetycznej w płaszczyźnie y = 0 reflektora wynosząmi( t )mi(�)
gdzie ω = 2Π f, f : częstotliwość, [Hz].
Zakładając bezstratną propagację fali, po przebyciu przez falę akustyczną odległości S KN , padające ciśnienie akustyczne p i (t) wynosi
a po przebyciu odległości SLMN ciśnienie akustyczne prefl (t) fali odbitej od substancji żrącej zgodnie z równaniem . ( 19 ) jest
Ciśnienie akustyczne pres ( t, θ ) wynikające z sumowania skalarnego fal dźwiękowych wynosi
Dalsza część tego punktu dotyczy zjawisk zachodzących w polu akustycznym.
Różnica dróg frontu bezpośredniego i odbitego fal akustycznych powoduje, że pres ( t, θ ) zmienia się w kaustyce w czasie. Fluktuacje są opisane równaniem. ( 30 ), który otrzymuje się przez podstawienie równań. ( 15 ), ( 16 ) do ( 26 ), ( 28 ), a następnie do ( 29 ).
Wahania mają postać modulacji amplitudy, której maksymalny zakres wynika z równania. ( 31 ).
Dla danego θ, równanie. ( 30 ) opisuje fluktuacje w danym punkcie kaustyki. Rozwiązywanie równania ( 31 ) czyli znalezienie funkcji t(θ), wyznacza amplitudę fluktuacji na całej kaustyce. Rozwiązanie równania ( 31 ) podano w równaniu. ( 32 ). Aby uzyskać szczegółowe informacje, patrz dodatek, równ. ( 49 ).
Gdzie
Podstawiając t do równania ( 30 ) daje maksymalny zakres modulacji amplitudy ciśnienia akustycznego pres ,Max ( θ ) [Pa] w całej kaustyce.
Studium przypadku
Mechanizm powstawania kaustyki i okoliczności powstawania ogniska, graficznie pokazane przez LdV na ryc. 1a , są pokazane w tej sekcji na rzeczywistych obiektach. Przedstawione przykłady dotyczą powstawania kaustyki wewnątrz i na zewnątrz instalacji akustycznych o funkcji demonstracyjnej. Pokazano również, w jaki sposób rozwój techniki odbiorczej związanej z detekcją fal radiowych rozszerzył aperturę zwierciadła oszacowaną za pomocą LdV.
Kaustyka w polu dźwiękowym
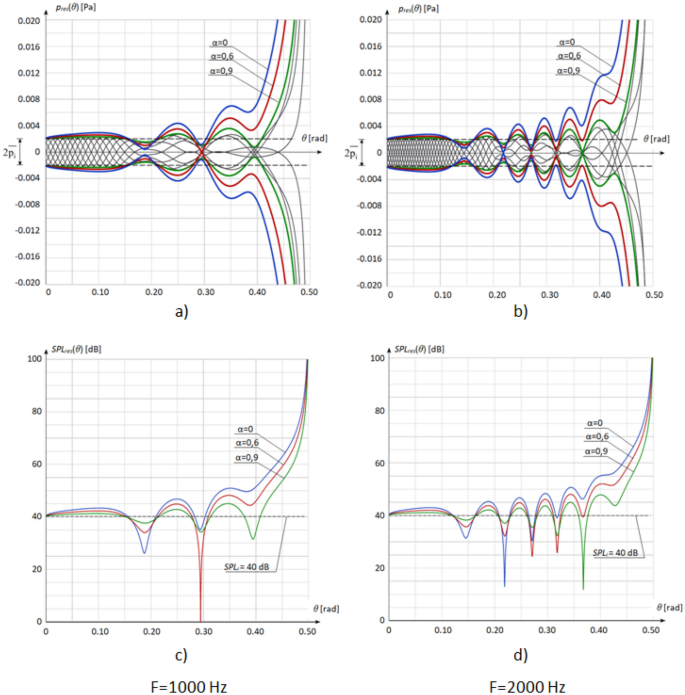
Rysunek 7 a, b przedstawia wykres równań. ( 30 ) i ( 34 ) dla fal dźwiękowych o częstotliwości f = 1000 Hz i f = 2000 Hz, odbitych od półkulistego reflektora o średnicy D = 2 m. W obu przypadkach długość fali λ jest znacznie mniejsza niż średnica reflektora D (odpowiednio λ/D = 0,17 i λ/D = 0,085). Kierunki fal pokazane na ryc. 6 spełniają więc zasady optyki geometrycznej, a dyfrakcję fali na krawędzi reflektora można pominąć.
a , b Wypadkowe ciśnienie akustyczne fal płaskich o częstotliwościach odpowiednio f = 1000 Hz i f = 2000 Hz, padających na półkulisty reflektor o promieniu R = 1 m i interferujących z falą tworzącą kaustykę. : amplituda padającej fali, α : współczynnik pochłaniania dźwięku reflektora. Cienkie czarne linie: ciśnienie akustyczne fali wypadkowej pres ( t , θ ) w punktach czasu t = 0, T/8, 7 T/8, gdzie T = 1/f, przy α = 0,9. Linie zielona, czerwona i niebieska: amplituda wahań pres ,Max ( θPI¯¯¯¯PI¯) odpowiednio przy α = 0,9, α = 0,6 i α = 0. Ze względu na symetrię pokazano zakres 0 ≤ θ ≤ Π/2. c , d Wypadkowy poziom ciśnienia akustycznego SPL res (θ) fal zakłócających opisanych powyżej. SPL i : poziom fali padającej.
Załóżmy, że natężenie padającej fali I o wynosi 10 –8 [W/m 2 ], co odpowiada ciśnieniu akustycznemu o amplitudzie 0,002 [Pa] i poziomie ciśnienia akustycznego SPL i = 40 dB re. 2 × 10 –5 [Pa] (Równania 35 , 36 ).
Ciśnienie akustyczne pres ( równanie 30 ) i odpowiadający mu poziom ciśnienia SPL res (równanie 37 ) oscylują wokół tych wartości. Amplituda fluktuacji wzrasta wraz ze wzrostem wpływu koncentracji fali na kaustykę (rys. 7 a, b).
Na wierzchołku kaustyki skoncentrowana energia fal odbitych znacznie przekracza energię fali padającej, co zmniejsza efekt fluktuacji (ryc. 7 c, d).
Efektem interferencji poza ogniskiem jest układ węzłów i antywęzłów powstały w wyniku nałożenia na soczewkę fal padających i odbitych. W rzeczywistych warunkach jego regularność pokazana na rys. 7 jest zaburzona przez szerokopasmowy charakter dźwięku oraz pole pogłosowe pomieszczenia. Jest to połączone z dyfrakcją padającej fali o niskiej częstotliwości na krawędzi czaszy. W efekcie obecność substancji żrących w pomieszczeniu jest zwykle trudna do wykrycia słuchem, a słyszalny efekt skupienia dźwięku przez lustra akustyczne zostaje zredukowany do zwartego obszaru o podwyższonym ciśnieniu akustycznym.
Rycina 7 pokazuje, jak dużego wzmocnienia dźwięku można się spodziewać na wierzchołku ługu. Gdy poziom dźwięku padającego na lustro wynosi około 40 dB, co odpowiada np. cichej rozmowie (rys. 7 c, d), poziom dźwięku odczuwanego w ognisku jest na tyle wysoki, że zjawisko to można wykorzystać do pokazów akustycznych lub do podsłuchiwania rozmów praktykowanych w czasach historycznych. Z rysunku 7 wynika, że w ognisku powierzchniowa gęstość mocy akustycznej może wzrosnąć o ok. 45 dB lub więcej, co odpowiada niewielkiej części czaszy. Jest to obliczeniowa ilustracja koncepcji LdV, jak pokazano na ryc. 2. Kąt otwarcia czaszy na oryginalnym rysunku LdV, z oczywistych względów niepopartych obliczeniami, wynosi ok. 10° .
Instalacje terenowe występujące w parkach edukacyjnych są współczesną realizacją obserwacji LdV (ryc. 8a ). Jaskinie szeptane pokazane na ryc. 8b , poza demonstracją efektu echa [ 10 ], służą również jako element historycznej architektury parkowej oraz miejsce schronienia przed deszczem. Dlatego ich kształt jest szerszy niż wymaga tego zademonstrowane zjawisko odbicia.
Instalacje plenerowe postawione w celu zademonstrowania ciekawostek akustycznych. a Współczesna instalacja plenerowa wykonana metodą druku 3D [ 15 , 16 , 17 ], fot. dzięki uprzejmości M. Kladeftira. b XVIII-wieczne Groty Szepczących w Parku Oliwskim, Gdańsk, Polska [ 10 , 14 ], fot. dzięki uprzejmości T. Struga
Istnieje wiele obiektów architektonicznych, w których formuje się kaustykę w formie pokazanej na rysunkach LdV. Mowa tu przede wszystkim o zabytkowych wnętrzach o funkcji sakralnej i ceremonialnej, zawierających duże powierzchnie w formie kopuły (ryc. 9 ). Kaustyka w opisanej formie powstawała również w dziewiętnastowiecznych teatrach i salach koncertowych ze sklepieniami wklęsłymi, które były wówczas kanonem stylu neorenesansowego (il. 10 ) [ 12 ].
Kaustyka w polach elektromagnetycznych
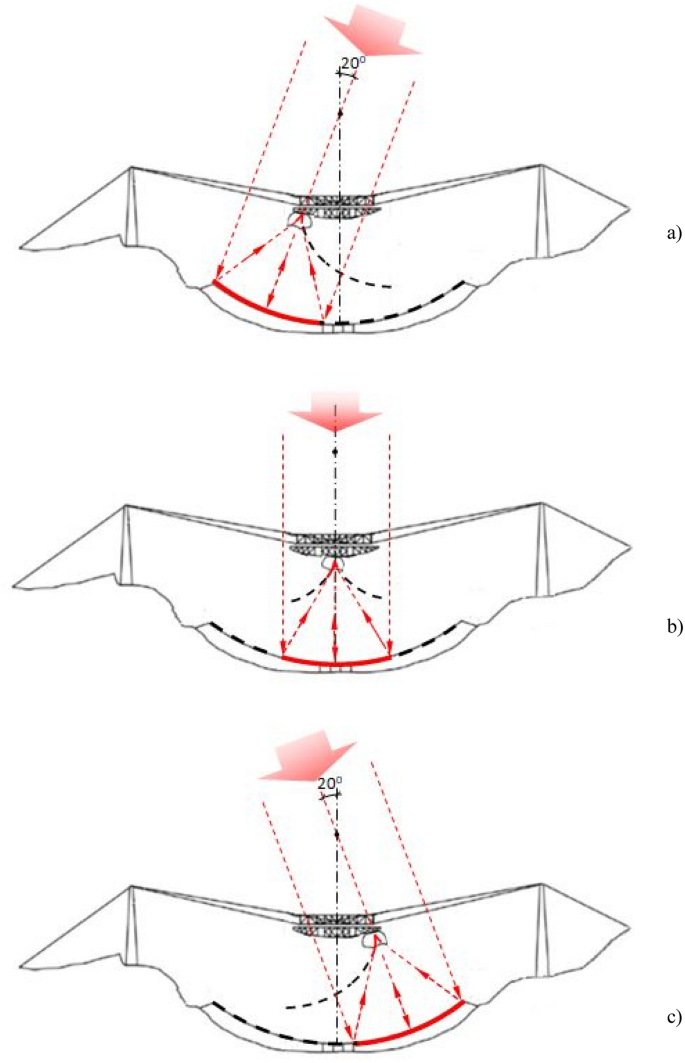
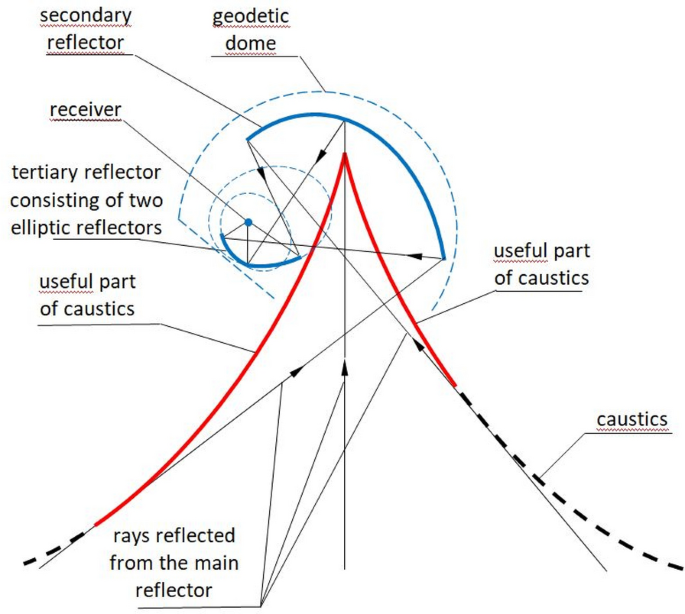
Radioteleskop Arecibo w Puerto Rico (ryc. 11 ) został oddany do użytku w 1963 roku i początkowo miał małą aperturę reflektora. Został znacznie ulepszony w 1997 roku przez zastosowanie systemu subreflektorów gregoriańskich, który koncentruje energię sekcji żrących sąsiadujących z wierzchołkiem w pojedynczym ognisku (ryc. 12 ) . System subreflektorów składa się z dwóch ukształtowanych powierzchni zwanych reflektorami drugorzędowymi i trzeciorzędnymi, ukrytych wewnątrz kopuły geodezyjnej. Pierwszy to reflektor paraboliczny, a drugi to para reflektorów eliptycznych (Rys. 13 ) [ 20 ].
Czasza odbłyśnika Arecibo i tworząca się w nim substancja żrąca. Aktywna część odbłyśnika i kaustyki jest pokazana (na czerwono). a , b , c Kierunki nadejścia fali − 20 o , 0 o , + 20 o względem zenitu. Szkic poglądowy na podstawie [ 20 ]
Śledzenie promieni drugorzędowych i trzeciorzędnych odbłyśników optyki gregoriańskiej Arecibo [ 23 ]. Oprócz energii ogniska, system subreflektorów gregoriańskich wykorzystuje również energię skupioną na części kaustycznej zaznaczonej na czerwono. Pokazano parę elips definiujących kształt reflektora trzeciorzędowego.
Zmodernizowana apertura radioteleskopu A Arecibo wynosi ok. 30 000 m 2 , czyli ok. 7% powierzchni półkuli o promieniu R Arecibo = 265 m (Równanie ( 38 )) [ 21 ].
W porównaniu z reflektorem analizowanym przez LdV o aperturze ok. 0,4% powierzchni półkuli (patrz rys. 3 , równania 1 i 2 ), względna apertura reflektora radioteleskopu Arecibo jest 17 razy większa (0,068/0,004 = 17), tj. o 1 rząd wielkości. Wynika to z faktu, że według LdV energia skupiona przez reflektor zawarta jest w jego ognisku, podczas gdy radioteleskop Arecibo powiększa ją o energię znacznej części substancji żrącej.
Przed modernizacją teleskopu Arecibo odbiornik rejestrował falę odbitą skoncentrowaną w ognisku oraz falę pochodzącą z kosmosu. Po doposażeniu teleskopu w subreflektory gregoriańskie, odbiornik ukryty wewnątrz kopuły geodezyjnej jest osłonięty odbłyśnikiem wtórnym oraz samą kopułą geodezyjną (Rys. 13) i nie rejestruje sygnału kosmicznego. Zmiana ta jest jednak pomijalna, gdyż poziom sygnału skupionego w ognisku przekracza poziom sygnału przestrzennego o kilkadziesiąt dB (patrz rys. 5 ) .
1 grudnia 2020 r. — tragiczny dzień dla środowiska naukowego — radioteleskop Arecibo został zniszczony w wyniku zerwania kabli i upadku 900-tonowej platformy głównej na czaszę radioteleskopu.
Odbłyśnik paraboliczny
W 2016 roku, 53 lata po uruchomieniu radioteleskopu w Arecibo, w Dawodang (Chiny) oddano do użytku radioteleskop FAST (Five-set-meter Aperture Spherical Radio Telescope). Jego antena o średnicy 520 m jest przekrojem kuli o promieniu R FAST = 300 m (rys. 14 ). Ważący 3 tony odbiornik, który porusza się po czaszy za pomocą systemu linek, umożliwia obserwację źródeł radiowych zawartych w stożku o kącie rozwarcia 80 stopni. Radioteleskop FAST jest urządzeniem odbiorczym, natomiast radioteleskop Arecibo był urządzeniem nadawczo-odbiorczym [ 25 ].
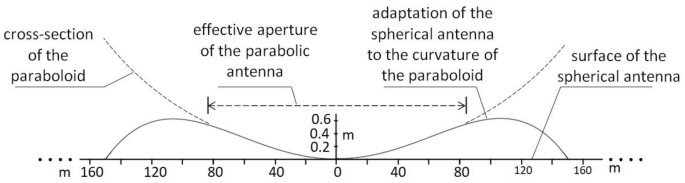
Czasza radioteleskopu FAST składa się z 4500 ruchomych elementów, których położenie można korygować w taki sposób, aby wybrana część sferycznego reflektora została przekształcona w segment paraboloidy (ryc. 15), w tym koło o średnicy 300 m. Skorygowana część reflektora tworzy zatem aperturę o średnicy A FAST = 300 m i głębokości D FAST = 40,2 m [ 26 ], co daje powierzchnię ok. 38.000 m 2 , czyli ok. 6,7% powierzchni półkuli (Równania 39 , 40). To pokazuje inny kierunek modernizacji koncepcji LdV w stosunku do Arecibo. Polega na manipulowaniu krzywizną odbłyśnika, podczas gdy w Arecibo manipulowano użytecznym zakresem żrącym.
Jedno z testowanych rozwiązań, pokazujące jak dopasować wycinek zwierciadła sferycznego radioteleskopu FAST do krzywizny paraboloidy [ 26 ]
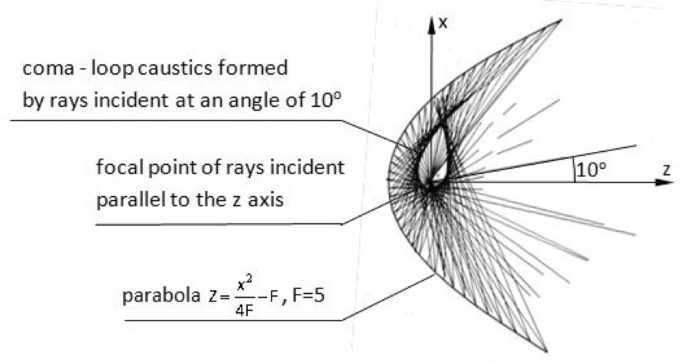
Obecna na rysunkach LdV kaustyka, zwana też aberracją sferyczną, traktowana jest jako ograniczenie w zastosowaniu zwierciadła sferycznego. W przypadku zwierciadła parabolicznego takim ograniczeniem jest aberracja koma. Występuje, gdy obserwowany obiekt znajduje się poza osią zwierciadła i polega na rozmyciu ogniska w pętlę kaustyczną zwaną śpiączką (ryc. 16 ). W zwierciadle sferycznym aberracja jest nieusuwalnym elementem jego funkcjonowania, natomiast w zwierciadle parabolicznym zanika całkowicie wraz z osiowym padaniem promieni. W radioteleskopie FAST aberracja koma jest ograniczana poprzez ustawienie odbiornika z dokładnością do kilku milimetrów, z odchyleniem od osi paraboloidy nieprzekraczającym 8 sekund kątowych [ 27 ] .
Przekrój zwierciadła parabolicznego z typowym zniekształceniem w postaci aberracji komatycznej. Gdy źródło znajduje się poza osią zwierciadła, ognisko przybiera postać pętli żrącej, znanej jako śpiączka [ 28 ]
Uwagi końcowe
W dorobku wielu wiodących dziedzin nauki odnaleźć można idee sprzed setek lat, często wywodzące się z dziedzin niezwiązanych z dziedziną. W artykule pokazano obecność koncepcji odbijania światła przez zwierciadło sferyczne, sformułowanej przez Leonarda da Vinci około 500 lat temu, w rozwoju pozornie odległych dziedzin nauki i techniki, takich jak akustyka czy radioastronomia.
Leonardo prowadził swoje badania teoretyczne za pomocą zwierciadła sferycznego. Pokazał, że wystarczy mniej niż 0,5% powierzchni półkuli, aby skoncentrować energię pochodzącą z nieskończenie odległego źródła, np. ze Słońca. Przy zastosowaniu tego lustra reszta czaszy jest bezużyteczna. Idea ta, oczywista z punktu widzenia współczesnej wiedzy, ale sformułowana 500 lat temu, jest obecna do dziś w wielu dziedzinach techniki i nauki – apertura współczesnych zwierciadeł sferycznych to tylko niewielka część półkuli. Ich funkcjonowanie w dziedzinie akustyki architektonicznej, w przyrządach optycznych, jako anteny w radioteleskopach itp. jest w pełni zgodne z przewidywaniami LdV.
Podczas badań nad zjawiskiem koncentracji światła LdV pokazał metodę graficznego wyznaczania towarzyszącej ognisku powierzchni, na której skupiają się promienie odbite. Powierzchnia ta jest dziś znana jako żrąca i jest obecna w wielu dziedzinach techniki i nauki. LdV jednak nie rozwinął idei kaustyki, najwyraźniej nieświadomy wagi swojego odkrycia. We współczesnej wiedzy technicznej można spotkać oba wyżej wymienione elementy funkcjonowania zwierciadeł odkrytych przez LdV, czyli ogniska i kaustykę. W przykładzie pokazanym w artykule dodanie energii kaustycznej do energii ogniskowej powoduje zwiększenie apertury od ok. 0,5% przewidywane przez LdV do ok. 5–7%. Po miejscowym dopasowaniu kulistej powierzchni zwierciadła do krzywizny paraboli, przysłona zwiększa się w podobnym stopniu. Apertura zwierciadła wyznaczona przez LdV została zatem znacznie ulepszona w wyniku rozwoju technik odbiorczych. Techniczną realizacją opisanych usprawnień są 300-metrowy radioteleskop w Arecibo (Portoryko) oraz 500-metrowy radioteleskop FAST w Dawodang (Chiny). Doniesienia internetowe informują o koncepcji budowy 1000-metrowego radioteleskopu, zlokalizowanego po ciemnej stronie Księżyca z dala od ziemskiego smogu elektromagnetycznego, jednak ze względu na wczesny etap realizacji tego pomysłu nie jest on omawiany w artykule [ Techniczną realizacją opisanych usprawnień są 300-metrowy radioteleskop w Arecibo (Portoryko) oraz 500-metrowy radioteleskop FAST w Dawodang (Chiny). Doniesienia internetowe informują o koncepcji budowy 1000-metrowego radioteleskopu, zlokalizowanego po ciemnej stronie Księżyca z dala od ziemskiego smogu elektromagnetycznego, jednak ze względu na wczesny etap realizacji tego pomysłu nie jest on omawiany w artykule [ Techniczną realizacją opisanych usprawnień są 300-metrowy radioteleskop w Arecibo (Portoryko) oraz 500-metrowy radioteleskop FAST w Dawodang (Chiny). Doniesienia internetowe informują o koncepcji budowy 1000-metrowego radioteleskopu, zlokalizowanego po ciemnej stronie Księżyca z dala od ziemskiego smogu elektromagnetycznego, jednak ze względu na wczesny etap realizacji tego pomysłu nie jest on omawiany w artykule [29 ].
Substancje żrące widoczne na rysunkach LdV powstają również w polu akustycznym we wnętrzach. Jednak zjawiska falowe występujące w pomieszczeniu, pogłos i szum tła utrudniają słyszalną identyfikację kaustyki. W rezultacie efekt ogniskowania dźwięku przez duże zakrzywione powierzchnie w pomieszczeniach, np. sklepienia łukowe i wklęsłe ściany, zostaje zredukowany do skupienia punktowego w ognisku żrącym, a pozostała część żrącej staje się niesłyszalna. Z tego powodu pojęcie kaustyki jest prawie nieznane w dziedzinie akustyki architektonicznej.
Dostępność danych i materiałów
Nie dotyczy.
Skróty
- LdV:
- Leonardo da Vinci
- SZYBKO:
- Sferyczny radioteleskop o aperturze pięciuset metrów
Bibliografia
-
http://www.unmuseum.org/burning_mirror.htm . Dostęp 29 września 2021 r.
-
https://en.wikipedia.org/wiki/Ptolemeusz . Dostęp 29 września 2021 r.
-
Raynauda Dominika. Perspektywa powietrzna Leonarda da Vinci i jego początki w optyce Ibn al-haythama (de aspektibus, III, 7). Arabscy filozofowie nauki. 2009;19(2):225–46.
-
Iwanow wiceprezes, Iwanowa GK. Żrąca struktura podwodnego kanału dźwiękowego. Otwórz Journal of Acoustics, 4, 26–37. 2014. http://file.scirp.org/pdf/OJA_2014032115460011.pdf . Dostęp 29 września 2021 r.
-
Khatkevich AG, Khatkevich LA. Propagacja wiązek laserowych i kaustyki w kryształach. Czasopismo spektroskopii stosowanej, 74, nr 4. 2007. https://link.springer.com/article/10.1007/s10812-007-0086-8 . Dostęp 29 września 2021 r.
-
Skowron J. Analiza niestandardowych zjawisk mikrosoczewkowania grawitacyjnego gwiazd Galaktyki. Rozprawa doktorska (Analiza niestandardowych zjawisk mikrosoczewkowania grawitacyjnego gwiazd Galaktyki. Rozprawa doktorska). Uniwersytet Warszawski. 2009. http://www.astrouw.edu.pl/~jskowron/PhD/thesis/phd.pdf . Dostęp 13 listopada 2021 r.
-
http://www.bl.uk/turning-the-pages/?id=cb4c06b9-02f4-49af-80ce540836464a46&type=book . Notatnik Leonarda, s. 8–15. Dostęp 29 września 2021 r.
-
http://www.bl.uk/turning-the-pages/?id=cb4c06b9-02f4-49af-80ce540836464a46&type=book,%20p.%208%E2%80%9314 , Kodeks Arundel Leonarda da Vinci, s. 224 –226, 414. Dostęp 29 września 2021 r.
-
Badania Leonarda da Vinci nad odbiciami od zwierciadeł wklęsłych ff.86v-87. strony11i12.html. http://www.bl.uk/onlinegallery/ttp/leonardo/accessible/ . Dostęp 08 czerwca 2022 r.
-
Kulowski A. Żrący w akustyce wnętrz zabytkowych. Dźwięk aplikacji. 2018;133:82–90. https://doi.org/10.1016/j.apacoust.2017.12.008 .
-
Badania Leonarda da Vinci nad odbiciami od zwierciadeł wklęsłych ff.87v-88. strony13i14.html. https://www.bl.uk/onlinegallery/ttp/leonardo/accessible/ . Dostęp 08 czerwca 2022 r.
-
Kulowski A. Analiza kaustyki utworzonej przez odbłyśnik sferyczny: wpływ kaustyki na akustykę architektoniczną. Dźwięk aplikacji. 2020. https://doi.org/10.1016/j.apacoust.2020.107333 .
-
Burkhard DG, Shealy DL. Wzór na gęstość promieni stycznych na żrącej powierzchni. Opcja aplikacji 1982;21(18):3299–306.
-
https://staraoliwa.pl/ . Dostęp 31 maja 2022 r.
-
https://dbt.arch.ethz.ch/project/acoustic-mirrors/ . Dostęp 16 sierpnia 2020 r.
-
Kladeftira M. i in. Strategie projektowe dla drukowanego w 3D akustycznego lustra Proc 24. konferencji CAADRIA – tom 1. Wellington: Victoria University of Wellington; 2019. s. 123–132.
-
Kladeftira M i in. Drukowanie naczyń szeptanych. Wielkoformatowe natryskiwanie spoiwa do instalacji zewnętrznych. Proc rekalibracji ACADIA 2018: o nieprecyzji i niewierności, Proc 38. dorocznej konferencji stowarzyszenia komputerowego wspomagania projektowania w architekturze. Meksyk; 2018. s. 328–35.
-
https://www.keepandshare.com/photo/382500/hagia-sophia?ifr=y . Dostęp 31 maja 2022 r.
-
http://poznanfilmcommission.pl/lokacja/aula-uam . Dostęp 21 września 2019 r.
-
https://www.researchgate.net/figure/A-diagram-of-the-Arecibo-telescope_fig1_2209614 . Dostęp 29 września 2021 r.
-
Magnani L. Mini-gregoriański system zasilania arecibo 5GHz; wydajność linii widmowej. Publ Astron Soc Pac. 1993;105(690):894–901.
-
https://www.space.com/38217-arecibo-observatory-puerto-rico-telescope-photos.html . Dostęp 29 września 2021 r.
-
Cortés-Medellín G. AOPAF: sygnał z układu fazowego obserwatorium arecibo. Publikacja internetowa Narodowego Centrum Astronomii i Jonosfery Uniwersytetu Cornell. 2010. https://www.naic.edu/~phil/hardware/byuPhasedAr/logs/Cortes%20AOPAF_short%20report%20Sept%202010-1.pdf . Dostęp 29 września 2021 r.
-
https://www.nature.com/articles/d41586-019-02790-3 . Dostęp 29 września 2021 r.
-
Mateusz JD. Krótka historia radaru geofizycznego w Obserwatorium Arecibo. Hist Geo- Sp Sci. 2013;4(1):19–33. https://doi.org/10.5194/hgss-4-19-2013 .
-
Nan R, Li D i in. Projekt radioteleskopu sferycznego o aperturze pięćset metrów (FAST), międzynarodowe czasopismo współczesnej fizyki D, © World Scientific Publishing Company. https://arxiv.org/ftp/arxiv/papers/1105/1105.3794.pdf . Dostęp 29 września 2021 r.
-
Williams II RL. „Pięćsetmetrowy sferyczny radioteleskop z aperturą (FAST) Model robota zawieszonego na kablu i porównanie z obserwatorium Arecibo”. www.ohio.edu/people/williar4/html/pdf/FAST.pdf . Dostęp 29 września 2021 r.
-
Schmidta RF. Analityczne powierzchnie żrące. Memorandum techniczne NASA 87805. Serwer raportów technicznych NASA. 1987. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19880001678.pdf . Dostęp 29 września 2021 r.
-
https://www.nasa.gov/directorates/spacetech/niac/2020_Phase_I_Phase_II/lunar_crater_radio_telescope/ . Dostęp 26 października 2021 r.
-
Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Al_Aqsa_(6888221391).jpg (przycięty). Dostęp 31 maja 2022 r.
Podziękowanie
Nie dotyczy
Finansowanie
Nie dotyczy.
Deklaracje etyczne
Konkurujące interesy
Autor oświadcza, że nie ma sprzecznych interesów.
Dodatkowe informacje
Uwaga wydawcy
Springer Nature pozostaje neutralny w odniesieniu do roszczeń jurysdykcyjnych na opublikowanych mapach i przynależności instytucjonalnej.
Załącznik
Załącznik
zastępowanie,
I
plony,
i po rozszerzeniu
przegrupowanie plonów,
i wtedy,
od,
Prawa i uprawnienia
Otwarty dostęp Ten artykuł jest objęty licencją Creative Commons Attribution 4.0 International License, która zezwala na używanie, dzielenie się, adaptację, dystrybucję i powielanie na dowolnym nośniku lub w dowolnym formacie, pod warunkiem, że podasz odpowiednie oznaczenie oryginalnego autora (autorów) i źródła, podać link do licencji Creative Commons i wskazać, czy dokonano zmian. Obrazy lub inne materiały osób trzecich zawarte w tym artykule są objęte licencją Creative Commons, chyba że zaznaczono inaczej w informacji o autorze materiału. Jeśli materiał nie jest objęty licencją Creative Commons, a zamierzone użycie jest niezgodne z przepisami prawa lub wykracza poza dozwolone użycie, musisz uzyskać pozwolenie bezpośrednio od właściciela praw autorskich. Aby zobaczyć kopię tej licencji, odwiedźhttp://creativecommons.org/licenses/by/4.0/.
Link do artykułu: https://heritagesciencejournal.springeropen.com/articles/10.1186/s40494-022-00713-6
Obraz wyróżniający: Arecibo radio telescope. Arecibo Observatory, Puerto Rico. Autorstwa Mariordo (Mario Roberto Durán Ortiz) – Praca własna, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=81590797